
【题目】下列各组函数中不表示同一函数的是( )
A.f(x)=lgx2 , g(x)=2lg|x|
B.f(x)=x,g(x)= ![]()
C.f(x)= ![]() ,g(x)=
,g(x)= ![]()
![]()
D.f(x)=|x+1|,g(x)= ![]()
【答案】C
【解析】解:对于A:f(x)=lgx2=2lg|x|的定义域为{x|x≠0},g(x)=2lg|x|的定义域为{x|x≠0},定义域相同,对应关系也相同,∴是同一函数;
对于B:f(x)=x的定义域为R,g(x)= ![]() =x的定义域为R,定义域相同,对应关系也相同,∴是同一函数;
=x的定义域为R,定义域相同,对应关系也相同,∴是同一函数;
对于C:f(x)= ![]() 的定义域为{x|x≥2或x≤﹣2},而g(x)=
的定义域为{x|x≥2或x≤﹣2},而g(x)= ![]()
![]() 的定义域为{x|x≥2},定义域不同,∴不是同一函数;
的定义域为{x|x≥2},定义域不同,∴不是同一函数;
对于D:f(x)=|x+1|= ![]() 的定义域为R,g(x)=
的定义域为R,g(x)= ![]() 的定义域为R,对应关系也相同,∴是同一函数;
的定义域为R,对应关系也相同,∴是同一函数;
故选:C.
【考点精析】解答此题的关键在于理解判断两个函数是否为同一函数的相关知识,掌握只有定义域和对应法则二者完全相同的函数才是同一函数.


 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:高中数学 来源: 题型:
【题目】今年入秋以来,某市多有雾霾天气,空气污染较为严重.市环保研究所对近期每天的空气污染情况进行调査研究后发现,每一天中空气污染指数与f(x)时刻x(时)的函数关系为f(x)=|log25(x+1)﹣a|+2a+1,x∈[0,24],其中a为空气治理调节参数,且a∈(0,1).
(1)若a= ![]() ,求一天中哪个时刻该市的空气污染指数最低;
,求一天中哪个时刻该市的空气污染指数最低;
(2)规定每天中f(x)的最大值作为当天的空气污染指数,要使该市每天的空气污染指数不超过3,则调节参数a应控制在什么范围内?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆C: ![]() 的离心率e=
的离心率e= ![]() ,左顶点M到直线
,左顶点M到直线 ![]() =1的距离d=
=1的距离d= ![]() ,O为坐标原点.
,O为坐标原点.
(1)求椭圆C的方程;
(2)设直线l与椭圆C相交于A,B两点,若以AB为直径的圆经过坐标原点,证明:点O到直线AB的距离为定值;
(3)在(2)的条件下,试求△AOB的面积S的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知⊙C:(x﹣1)2+(y﹣2)2=25,直线l:(2m+1)x+(m+1)y﹣7m﹣4=0(m∈R)
(1)求证:对任意m∈R,直线l与⊙C恒有两个交点;
(2)求直线l被⊙C截得的线段的最短长度,及此时直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知四棱锥P﹣ABCD的底面为直角梯形,AB∥DC,∠DAB=90°,PA⊥底面 ABCD,且PA=AD=DB= ![]() ,AB=1,M是PB的中点.
,AB=1,M是PB的中点. 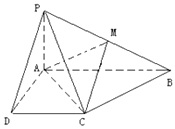
(1)证明:面PAD⊥面PCD;
(2)求AC与PB所成的角;
(3)求平面AMC与平面BMC所成二面角的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义运算为:a*b= ![]() ,如1*2=1,则函数f(x)=|2x*2﹣x﹣1|的值域为( )
,如1*2=1,则函数f(x)=|2x*2﹣x﹣1|的值域为( )
A.[0,1]
B.[0,1)
C.[0,+∞)
D.[1,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】各项均为正数的数列{an}中,a1=1,Sn是数列{an}的前n项和,对任意n∈N* , 有2Sn=2pan2+pan﹣p(p∈R)
(1)求常数p的值;
(2)求数列{an}的通项公式;
(3)记bn= ![]() ,求数列{bn}的前n项和T.
,求数列{bn}的前n项和T.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com