
分析 (1)设F′为椭圆的左焦点,连结MF′,作过P、F′的直线交椭圆于M1、M2两点.根据椭圆的定义算出|MP|+|MF|=|MP|+(2a-|MF'|)=4+(|MP|-|MF′|),由平面几何知识得-|PF′|≤|MP|-|MF′|≤|PF′|,再利用两点间的距离公式加以计算,即可得到|MP|+|MF|的取值范围.
(2)设P(x0,y0)(y0≠0),即可得出直线AP的方程,令x=2,即可得到点M的坐标,利用斜率计算公式即可得出k1,k2,再利用点P在椭圆上即可证明;
(3)设A(x1,y1),B(x2,y2),AB:x=my-1,代入椭圆方程$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$,得(3m2+4)y2-6my-9=0,由此利用已知条件能证明以线段CD为直径的圆过x轴上的两个定点(-1,0)和(-7,0).
(4)设出点的坐标,表示出kPM、kPN,即可证明kPM•kPN为定值.
(5)将直线l的方程y=kx+m代入椭圆C的方程3x2+4y2=12中,得到关于x的一元二次方程,由直线l与椭圆C仅有一个公共点知,△=0,即可得到m,k的关系式,利用点到直线的距离公式即可得到d1=|F1M|,d2=|F2N|.
法一:当k≠0时,设直线l的倾斜角为θ,则|d1-d2|=|MN|×|tanθ|,即可得到四边形F1MNF2面积S的表达式,利用基本不等式的性质即可得出S的最大值;
法二:利用d1及d2表示出${d}_{1}^{2}+{d}_{2}^{2}$及d1d2,进而得到${S^2}=\frac{1}{{{k^2}+1}}({d_1}^2+{d_2}^2+2{d_1}{d_2})=\frac{{16{k^2}+12}}{{{{({k^2}+1)}^2}}}$,再利用二次函数的单调性即可得出其最大值.
(6)存在这样的点M符合题意.设线段PQ的中点为N,P(x1,y1),Q(x2,y2),N(x0,y0),直线PQ的斜率为k(k≠0),注意到F2(1,0),则直线PQ的方程为y=k(x-1),与椭圆方程联立得到根与系数的关系,利用中点坐标公式即可得到点N,再利用向量$\overrightarrow{QP}•\overrightarrow{MP}=\overrightarrow{PQ}•\overrightarrow{MQ}$可得$\overrightarrow{PQ}•(\overrightarrow{MP}+\overrightarrow{MQ})=2\overrightarrow{PQ}•\overrightarrow{MN}=0$,因此PQ⊥MN,利用k•kMN=-1即可得到m与k的关系.
(7)不存在.可用反证法证明.若这样的三角形存在,由题可设$P(\frac{{{y_1}^2}}{4},{y_1})({y_1}≠0),M({x_2},{y_2})$,由条件知点M在椭圆上可得$\frac{{{x_2}^2}}{4}+\frac{{{y_2}^2}}{3}=1$,由三角形的重心定理可得$\overrightarrow{OA}+\overrightarrow{OP}+\overrightarrow{OM}=\overrightarrow 0$,及点A(-2,0),代入化简即可得到x2,判断即可.
解答 解:(1)设F′为椭圆的左焦点,连结MF′,作过P、F′的直线交椭圆于M1、M2两点,如图所示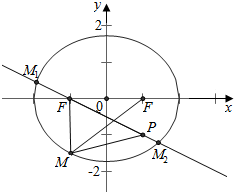
∵$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$中,a=2,b=$\sqrt{3}$,
∴c=$\sqrt{{a}^{2}-{b}^{2}}$=1,可得F(1,0),F′(-1,0).
由椭圆的定义,得|MF|+|MF′|=2a=4,
∴|MP|+|MF|=|MP|+(4-|MF′|)=4+(|MP|-|MF′|)
由平面几何知识,得-|PF′|≤|MP|-|MF′|≤|PF′|,
∴当M与M1重合时,|MP|-|MF′|达到最大值|PF′|;当M与M2重合时,|MP|-|MF′|达到最小值-|PF′|.
由|PF′|=$\sqrt{(1+1)^{2}+(-1-0)^{2}}$=$\sqrt{5}$,可得|MP|-|MF′|的最大值为$\sqrt{5}$,最小值为-$\sqrt{5}$.
∴|MP|+|MF|=4+(|MP|-|MF′|)的取值范围为[4-$\sqrt{5}$,4+$\sqrt{5}$].
(2))设P(x1,y1)(y1≠0),M(2,y0),则${k_1}=\frac{y_0}{2}$,${k_2}=\frac{y_1}{{{x_1}-2}}$,
∵A,P,M三点共线,∴${y_0}=\frac{{4{y_1}}}{{{x_1}+2}}$,
设直线BP的斜率为${k_2}=\frac{y_1}{{{x_1}-2}}$,直线m的斜率为${k_m}=\frac{{2-{x_1}}}{y_1}$,
则直线m的方程为$y-{y_0}=\frac{{2-{x_1}}}{y_1}(x-2)$,$y=\frac{{2-{x_1}}}{y_1}(x-2)+{y_0}=\frac{{2-{x_1}}}{y_1}x-\frac{{2(2-{x_1})}}{y_1}+\frac{{4{y_1}}}{{{x_1}+2}}$=$\frac{{2-{x_1}}}{y_1}x+\frac{{2({x_1}^2-4)+4y_1^2}}{{({x_1}+2){y_1}}}$=$\frac{{2-{x_1}}}{y_1}x+\frac{{2({x_1}^2-4)+12-3x_1^2}}{{({x_1}+2){y_1}}}$
=$\frac{{2-{x_1}}}{y_1}x+\frac{{2-{x_1}}}{y_1}$=$\frac{{2-{x_1}}}{y_1}(x+1)$,
即$y=\frac{2-{x}_{1}}{{y}_{1}}(x+1)$.
所以直线m过定点(-1,0).
(3)证明:设A(x1,y1),B(x2,y2),AB:x=my-1,
代入椭圆方程$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$,整理,得(3m2+4)y2-6my-9=0,
∴$\left\{\begin{array}{l}{{y}_{1}+{y}_{2}=\frac{6m}{3{m}^{2}+4}}\\{{y}_{1}{y}_{2}=\frac{-9}{3{m}^{2}+4}}\end{array}\right.$,
∵MC:y=$\frac{{y}_{1}}{{x}_{1}-2}(x-2)$,∴${y}_{C}=\frac{-6{y}_{1}}{{x}_{1}-2}$,
∵MD:y=$\frac{{y}_{2}}{{x}_{2}-2}(x-2)$,∴${y}_{D}=\frac{-6{y}_{2}}{{x}_{2}-2}$,
∴${y}_{C}{y}_{D}=\frac{36{y}_{1}{y}_{2}}{({x}_{1}-2)({x}_{2}-2)}$=$\frac{36{y}_{1}{y}_{2}}{(m{y}_{1}-3)(m{y}_{2}-3)}$
=$\frac{36{y}_{1}{y}_{2}}{{m}^{2}{y}_{1}{y}_{2}-3m({y}_{1}+{y}_{2})+9}$
=$\frac{36•\frac{-9}{3{m}^{2}+4}}{{m}^{2}•\frac{-9}{3{m}^{2}+4}-3m•\frac{6m}{3{m}^{2}+4}+9}=-9$,
设CD与x轴交于点N,以线段CD为直径的圆与x轴交于点P,Q,
则NP2=NQ2=NC•ND=|yCyD|=9,NP=NQ=3,
∵N(-4,0),∴点P,Q的坐标为(-1,0),(-7,0),
∴以线段CD为直径的圆过x轴上的两个定点(-1,0)和(-7,0).
证明:设M、N是椭圆上关于原点对称点,设M(x0,y0),则N(-x0,-y0),
(4)设P点坐标为(x,y),则$\frac{{x}_{0}^{2}}{{a}^{2}}+\frac{{y}_{0}^{2}}{{b}^{2}}=1$,
$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1.
即${y}_{0}^{2}={b}^{2}(1-\frac{{x}_{0}^{2}}{{a}^{2}})=\frac{{b}^{2}}{{a}^{2}}?({a}^{2}-{x}_{0}^{2})$,${y}^{2}={b}^{2}(1-\frac{{x}^{2}}{{a}^{2}})=\frac{{b}^{2}}{{a}^{2}}?({a}^{2}-{x}^{2})$,
∴$k_{PM}^{\;}•{k_{PN}}=\frac{{y-{y_0}}}{{x-{x_0}}}•\frac{{y+{y_0}}}{{x+{x_0}}}=\frac{{{y^2}-y_0^2}}{{{x^2}-x_0^2}}$=$\frac{\frac{{b}^{2}}{{a}^{2}}?({a}^{2}-{x}^{2})-\frac{{b}^{2}}{{a}^{2}}?({a}^{2}-{x}_{0}^{2})}{{x}^{2}-{x}_{0}^{2}}$=$-\frac{{b}^{2}}{{a}^{2}}$为定值.
(5)将直线l的方程y=kx+m代入椭圆C的方程3x2+4y2=12中,得(4k2+3)x2+8kmx+4m2-12=0.
由直线l与椭圆C仅有一个公共点知,△=64k2m2-4(4k2+3)(4m2-12)=0,
化简得:m2=4k2+3.
设${d_1}=|{{F_1}M}|=\frac{{|{-k+m}|}}{{\sqrt{{k^2}+1}}}$,${d}_{2}=|{F}_{2}N|=\frac{|k+m|}{\sqrt{{k}^{2}+1}}$,
法一:当k≠0时,设直线l的倾斜角为θ,
则|d1-d2|=|MN|×|tanθ|,
∴$|{MN}|=|{\frac{{{d_1}-{d_2}}}{k}}|$,$S=\frac{1}{2}|{\frac{{{d_1}-{d_2}}}{k}}|({d_1}+{d_2})=|{\frac{{{d_1}^2-{d_2}^2}}{2k}}|=\frac{2|m|}{{{k^2}+1}}$=$\frac{2|m|}{{\frac{{{m^2}-3}}{4}+1}}=\frac{8}{{|m|+\frac{1}{|m|}}}$,
∵m2=4k2+3,∴当k≠0时,$|m|>\sqrt{3}$,$|m|+\frac{1}{|m|}>\sqrt{3}+\frac{1}{{\sqrt{3}}}=\frac{4}{3}\sqrt{3}$,$S<2\sqrt{3}$.
当k=0时,四边形F1MNF2是矩形,$S=2\sqrt{3}$.
所以四边形F1MNF2面积S的最大值为$2\sqrt{3}$.
法二:∵${d_1}^2+{d_2}^2={(\frac{{|{-k+m}|}}{{\sqrt{{k^2}+1}}})^2}+{(\frac{{|{k+m}|}}{{\sqrt{{k^2}+1}}})^2}=\frac{{2({m^2}+{k^2})}}{{{k^2}+1}}=\frac{{2(5{k^2}+3)}}{{{k^2}+1}}$,${d_1}{d_2}=\frac{{|{-k+m}|}}{{\sqrt{{k^2}+1}}}•\frac{{|{k+m}|}}{{\sqrt{{k^2}+1}}}=\frac{{|{{m^2}-{k^2}}|}}{{{k^2}+1}}=\frac{{3{k^2}+3}}{{{k^2}+1}}=3$.
∴$|{MN}|=\sqrt{{F_1}{F_2}^2-{{({d_1}-{d_2})}^2}}$=$\sqrt{4-({d_1}^2+{d_2}^2-2{d_1}{d_2})}=\frac{2}{{\sqrt{{k^2}+1}}}$.
四边形F1MNF2的面积$S=\frac{1}{2}|{MN}|({d_1}+{d_2})$=$\frac{1}{{\sqrt{{k^2}+1}}}({d_1}+{d_2})$,
${S^2}=\frac{1}{{{k^2}+1}}({d_1}^2+{d_2}^2+2{d_1}{d_2})=\frac{{16{k^2}+12}}{{{{({k^2}+1)}^2}}}$=$16-4{(\frac{1}{{{k^2}+1}}-2)^2}≤12$.
当且仅当k=0时,${S^2}=12,S=2\sqrt{3}$,故${S_{max}}=2\sqrt{3}$.
所以四边形F1MNF2的面积S的最大值为$2\sqrt{3}$.
(6)存在这样的点M符合题意.设线段PQ的中点为N,P(x1,y1),Q(x2,y2),N(x0,y0),
直线PQ的斜率为k(k≠0),注意到F2(1,0),则直线PQ的方程为y=k(x-1),
由$\left\{\begin{array}{l}{\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1}\\{y=k(x-1)}\end{array}\right.$消去y得:(4k2+3)x2-8k2x+4k2-12=0,
所以${x}_{1}+{x}_{2}=\frac{8{k}^{2}}{4{k}^{2}+3}$,
故${x}_{0}=\frac{{x}_{1}+{x}_{2}}{2}=\frac{4{k}^{2}}{4{k}^{2}+3}$,y0=k(x0-1)=$\frac{-3k}{4{k}^{2}+3}$.
又点N在直线PQ上,所以N$(\frac{4{k}^{2}}{4{k}^{2}+3},\frac{-3k}{4{k}^{2}+3})$,
由$\overrightarrow{QP}•\overrightarrow{MP}=\overrightarrow{PQ}•\overrightarrow{MQ}$可得$\overrightarrow{PQ}•(\overrightarrow{MP}+\overrightarrow{MQ})=2\overrightarrow{PQ}•\overrightarrow{MN}=0$,
∴PQ⊥MN,∴kMN=$\frac{0+\frac{3k}{4{k}^{2}+3}}{m-\frac{4{k}^{2}}{4{k}^{2}+3}}=-\frac{1}{k}$,
整理得$m=\frac{{k}^{2}}{4{k}^{2}+3}$=$\frac{1}{4+\frac{3}{{k}^{2}}}$$∈(0,\frac{1}{4})$,
所以,在线段OF2上存在点M(m,0)符合题意,其中$m∈(0,\frac{1}{4})$.
(7)不存在,理由如下:若这样的三角形存在,由题可设$P(\frac{{{y_1}^2}}{4},{y_1})({y_1}≠0),M({x_2},{y_2})$,
由条件①知$\frac{{{x_2}^2}}{4}+\frac{{{y_2}^2}}{3}=1$,
由条件②得$\overrightarrow{OA}+\overrightarrow{OP}+\overrightarrow{OM}=\overrightarrow 0$,又因为点A(-2,0),
所以$\left\{\begin{array}{l}\frac{{{y_1}^2}}{4}+{x_2}-2=0\\{y_1}+{y_2}=0\end{array}\right.$即$\frac{{{y_2}^2}}{4}+{x_2}-2=0$,
故$\frac{3}{4}-\frac{3}{16}{x_2}^2+{x_2}-2=0$,
解之得x2=2或${x_2}=\frac{10}{3}$(舍),
当x2=2时,解得P(0,0)不合题意,
所以同时满足两个条件的三角形不存在.
点评 本题主要考查椭圆的方程与性质、直线方程、直线与椭圆的位置关系、等差数列、二次函数的单调性、基本不等式的性质等基础知识,考查运算能力、推理论证以及分析问题、解决问题的能力,考查数形结合、化归与转化思想.综合性较强,难度较大.


科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 2 | C. | $\sqrt{3}$ | D. | $\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
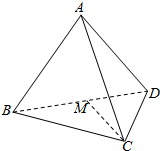 如图,在三棱锥A-BCD中,等边△BCD的边长为4,△ABD是以∠A为直角的等腰直角三角形,平面ABD⊥平面BCD,点M是棱BD的中点.
如图,在三棱锥A-BCD中,等边△BCD的边长为4,△ABD是以∠A为直角的等腰直角三角形,平面ABD⊥平面BCD,点M是棱BD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com