Question

【题目】已知等差数列{an}前三项的和为﹣3，前三项的积为8．
（I）求等差数列{an}的通项公式；
（II）若a2 ， a3 ， a1成等比数列，求数列{|an|}的前n项和．

Answer 1

【答案】解：（I）设等差数列的公差为d，则a2=a1+d，a3=a1+2d
由题意可得，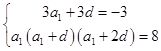
解得 或
由等差数列的通项公式可得，an=2﹣3（n﹣1）=﹣3n+5或an=﹣4+3（n﹣1）=3n﹣7
（II）当an=﹣3n+5时，a2 ， a3 ， a1分别为﹣1，﹣4，2不成等比
当an=3n﹣7时，a2 ， a3 ， a1分别为﹣1，2，﹣4成等比数列，满足条件
故|an|=|3n﹣7|=
设数列{|an|}的前n项和为Sn
当n=1时，S1=4，当n=2时，S2=5
当n≥3时，Sn=|a1|+|a2|+…+|an|=5+（3×3﹣7）+（3×4﹣7）+…+（3n﹣7）
=5+ = ，当n=2时，满足此式
综上可得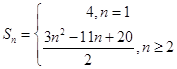
【解析】（I）设等差数列的公差为d，由题意可得， ，解方程可求a1 ， d，进而可求通项（II）由（I）的通项可求满足条件a2 ， a3 ， a1成等比的通项为an=3n﹣7，则|an|=|3n﹣7|= ，根据等差数列的求和公式可求