
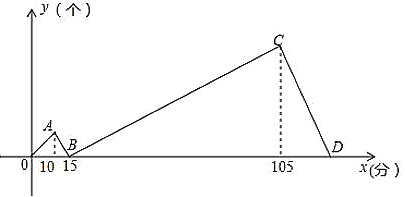
【题目】甲乙两人同时各接受了600个零件的加工任务,甲比乙每分钟加工的数量多,两人同时开始加工,加工过程中甲因故障停止一会后又继续按原速加工,直到他们完成任务.如图表示甲比乙多加工的零件数量y(个)与加工时间x(分)之间的函数关系,A点横坐标为10,B点坐标为![]() ,C点横坐标为105.则甲每分钟加工的数量是_______,点D的坐标是_______.
,C点横坐标为105.则甲每分钟加工的数量是_______,点D的坐标是_______.
科目:高中数学 来源: 题型:
【题目】已知二次函数![]()
(1)若函数在区间![]() 上存在零点,求实数
上存在零点,求实数![]() 的取值范围;
的取值范围;
(2)是否存在常数![]() ,当
,当![]() 时,
时,![]() 的值域为区间
的值域为区间![]() ,且区间
,且区间![]() 的长度为
的长度为![]() (视区间
(视区间![]() 的长度为
的长度为![]() ),如果存在,求出
),如果存在,求出![]() 的值;如果不存在,说明理由.
的值;如果不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有![]() 名乒乓球选手进行单循环赛(无和局),比赛结果显示:任意5人中既有1人胜于其余4人,又有1人负于其余4人.则恰胜两场的人数为______个.
名乒乓球选手进行单循环赛(无和局),比赛结果显示:任意5人中既有1人胜于其余4人,又有1人负于其余4人.则恰胜两场的人数为______个.
查看答案和解析>>
科目:高中数学 来源: 题型:
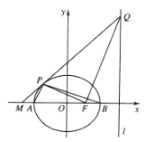
【题目】如图,在平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() 的右准线方程
的右准线方程![]() ,离心率
,离心率![]() ,左、右顶点分别为A,B,右焦点为F,点P在椭圆上,且位于x轴上方.
,左、右顶点分别为A,B,右焦点为F,点P在椭圆上,且位于x轴上方.
(Ⅰ)设直线![]() 的斜率为
的斜率为![]() ,直线
,直线![]() 的斜率为
的斜率为![]() ,求
,求![]() 的最小值;
的最小值;
(Ⅱ)点Q在右准线l上,且![]() ,直线
,直线![]() 交x负半轴于点M,若
交x负半轴于点M,若![]() ,求点P坐标.
,求点P坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某班在一次个人投篮比赛中,记录了在规定时间内投进![]() 个球的人数分布情况:
个球的人数分布情况:
进球数 | 0 | 1 | 2 | 3 | 4 | 5 |
投进 | 1 | 2 | 7 | 2 |
其中![]() 和
和![]() 对应的数据不小心丢失了,已知进球3个或3个以上,人均投进4个球;进球5个或5个以下,人均投进2.5个球.
对应的数据不小心丢失了,已知进球3个或3个以上,人均投进4个球;进球5个或5个以下,人均投进2.5个球.
(1)投进3个球和4个球的分别有多少人?
(2)从进球数为3,4,5的所有人中任取2人,求这2人进球数之和为8的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校开展主题为“垃圾分类,绿色生活新时尚”的宣传活动,为了解学生对垃圾分类知识的掌握情况,该校环保社团成员在校园内随机抽取了部分学生进行问卷调查,将他们的得分按优秀、良好、合格、待合格四个等级进行统计,并绘制了如下不完整的统计表和条形统计图.请根据以下信息,解答下列问题:
等级 | 频数 | 频率 |
优秀 | 21 | 42% |
良好 |
| 40% |
合格 | 6 |
|
待合格 | 3 | 6% |
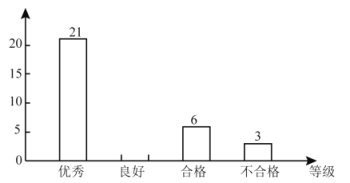
(1)本次调查随机抽取了__________名学生,表中![]() __________,
__________,![]() __________;
__________;
(2)补全条形统计图;
(3)若全校有![]() 名学生,请你估计该校掌握垃圾分类知识达到“优秀”和“良好”等级的学生共有多少人.
名学生,请你估计该校掌握垃圾分类知识达到“优秀”和“良好”等级的学生共有多少人.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com