
分析 (Ⅰ)利用对数性质、运算法则求解.
(Ⅱ)利用三角函数定义先求出正切,再利用诱导公式、同角三角函数关系式能求出结果.
解答 解:(I)${log_{\frac{1}{3}}}\sqrt{27}+lg25+lg4+{7^{-{{log}_7}2}}+{(-0.98)^0}$
=$lo{g}_{\frac{1}{3}}{3}^{\frac{3}{2}}$+lg100+${7}^{lo{g}_{7}\frac{1}{2}}$+1
=-$\frac{3}{2}+2+\frac{1}{2}+1$
=2.
(II)∵角α的终边上一点$P(\sqrt{2},-\sqrt{6})$,
∴由题得tanα=$\frac{-\sqrt{6}}{\sqrt{2}}$=-$\sqrt{3}$,
∴$\frac{{cos(\frac{π}{2}+α)cos(2π-α)+sin(-α-\frac{π}{2})cos(π-α)}}{{sin(π+α)cos(\frac{π}{2}-α)}}$
=$\frac{-sinαcosα+(-cosα)(_cosα)}{-sinαsinα}$
=$\frac{sinαcosα-co{s}^{2}α}{si{n}^{2}α}$
=$\frac{tanα-1}{ta{n}^{2}α}$=-$\frac{\sqrt{3}+1}{3}$.
点评 本题考查对数式、三角函数式化简求值,是基础题,解题时要认真审题,注意对数性质、运算法则、三角函数定义、诱导公式、同角三角函数关系式的合理运用.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{{x}^{2}}{4}$-y2=1 | B. | x2-$\frac{{y}^{2}}{4}$=1 | C. | $\frac{3{x}^{2}}{20}$-$\frac{3{y}^{2}}{5}$=1 | D. | $\frac{3{x}^{2}}{5}$-$\frac{3{y}^{2}}{20}$=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
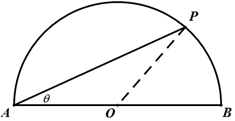 运动员小王在一个如图所示的半圆形水域(O为圆心,AB是半圆的直径)进行体育训练,小王先从点A出发,沿着线段AP游泳至半圆上某点P处,再从点P沿着弧PB跑步至点B处,最后沿着线段BA骑自行车回到点A处,本次训练结束.已知OA=1500m,小王游泳、跑步、骑自行车的平均速度分别为2m/s,4m/s,10m/s,设∠PAO=θrad.
运动员小王在一个如图所示的半圆形水域(O为圆心,AB是半圆的直径)进行体育训练,小王先从点A出发,沿着线段AP游泳至半圆上某点P处,再从点P沿着弧PB跑步至点B处,最后沿着线段BA骑自行车回到点A处,本次训练结束.已知OA=1500m,小王游泳、跑步、骑自行车的平均速度分别为2m/s,4m/s,10m/s,设∠PAO=θrad.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{22}{7}$ | B. | $\frac{25}{8}$ | C. | $\frac{23}{7}$ | D. | $\frac{157}{50}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{5}}{5}$ | B. | ±$\frac{2\sqrt{5}}{5}$ | C. | -$\frac{\sqrt{5}}{5}$ | D. | $\frac{2\sqrt{5}}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $x+\sqrt{3}y=2$ | B. | $\sqrt{3}x+y=2$ | C. | $x+\sqrt{3}y=1$ | D. | $\sqrt{3}x+y=1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | M∩N={(-1,1)} | B. | M∩N=∅ | C. | M⊆N | D. | N⊆M |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com