
【题目】把1、2、3、4、5这五个数字组成无重复数字的五位数,并把它们由小大到的顺序排成一个数列.
(Ⅰ)求![]() 是这个数列的第几项;
是这个数列的第几项;
(Ⅱ)求这个数列的第96项;
(Ⅲ)求这个数列的所有项和.
【答案】(1)第![]() 项.(2)
项.(2)![]() .(3)
.(3)![]() .
.
【解析】试题分析:(1)可从反面出发:大于![]() 的数可分为以下三类:以5开头,以45开头,以435开头,最后用
的数可分为以下三类:以5开头,以45开头,以435开头,最后用![]() 减即得,(2)比第
减即得,(2)比第![]() 项所表示的五位数大的五位数有
项所表示的五位数大的五位数有![]() 个,而以5开头的有
个,而以5开头的有![]() (个),所以第
(个),所以第![]() 项为
项为![]() (3)每位数字之和为
(3)每位数字之和为![]() ,共有
,共有![]() (个),所以所有项和为
(个),所以所有项和为![]()
试题解析:
(Ⅰ)大于![]() 的数可分为以下三类:
的数可分为以下三类:
第一类:以5开头的有![]() (个),第二类:以45开头的有
(个),第二类:以45开头的有![]() (个),第三类:以435开头的有
(个),第三类:以435开头的有![]() (个),
(个),
故不大于![]() 的五位数有
的五位数有![]() (个),即
(个),即![]() 是第
是第![]() 项.
项.
(Ⅱ)数列共有![]() 项,
项, ![]() 项之后还有
项之后还有![]() 项。
项。
即比第![]() 项所表示的五位数大的五位数有
项所表示的五位数大的五位数有![]() 个,
个,
∴小于![]() 开头的五位数中最大的一个就是该数列的第
开头的五位数中最大的一个就是该数列的第![]() 项,即为
项,即为![]() .
.
(Ⅲ)∵![]() 各在万位上时都有
各在万位上时都有![]() 个五位数,∴万位上数字的和为
个五位数,∴万位上数字的和为![]() ,
,
同理![]() 在千位、百位、十位、个位上也有
在千位、百位、十位、个位上也有![]() 个五位数,∴这个数列的所有项和为
个五位数,∴这个数列的所有项和为
![]() .
.


科目:高中数学 来源: 题型:
【题目】如图,三棱柱![]() 的底面是边长为2的正三角形且侧棱垂直于底面,侧棱长是
的底面是边长为2的正三角形且侧棱垂直于底面,侧棱长是![]() ,
, ![]() 是
是![]() 的中点.
的中点.

(1)求证: ![]() 平面
平面![]() ;
;
(2)求二面角![]() 的大小;
的大小;
(3)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在多面体ABCDEF中,底面ABCD是梯形,四边形ADEF是正方形,AB∥DC,AB=AD=1,CD=2,AC=EC=![]() 。
。
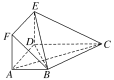
(1)求证:平面EBC⊥平面EBD;
(2)设M为线段EC上一点,且3EM=EC,试问在线段BC上是否存在一点T,使得MT∥平面BDE,若存在,试指出点T的位置;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市某水产养殖户进行小龙虾销售,已知每千克小龙虾养殖成本为6元,在整个销售旺季的80天里,销售单价![]() (元/千克)与时间第
(元/千克)与时间第![]() (天)之间的函数关系为:
(天)之间的函数关系为:
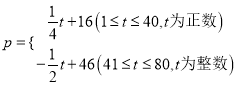 ,日销售量
,日销售量![]() (千克)与时间第
(千克)与时间第![]() (天)之间的函数关系如图所示:
(天)之间的函数关系如图所示:
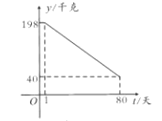
(1)求日销售量![]() 与时间
与时间![]() 的函数关系式?
的函数关系式?
(2)哪一天的日销售利润最大?最大利润是多少?
(3)在实际销售的前40天中,该养殖户决定每销售1千克小龙虾,就捐赠![]() 元给村里的特困户,在这前40天中,每天扣除捐赠后的日销售利润随时间
元给村里的特困户,在这前40天中,每天扣除捐赠后的日销售利润随时间![]() 的增大而增大,求
的增大而增大,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com