
下列是真命题的命题序号是 .
①分别表示空间向量的有向线段所在的直线是异面直线,则这两个向量不是共面向量
②若|a|=|b|,则a,b的长度相等而方向相同或相反
③若向量 ,
, 满足|
满足| |>|
|>| |,且
|,且 与
与 同向,则
同向,则 >
>
④若两个非零向量 与
与 满足
满足 +
+ =
= ,则
,则 ∥
∥
科目:高中数学 来源: 题型:
| 1 |
| 2 |
| 1-cosx |
| 2 |
| x |
| 2 |
| π |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
|
| 1 |
| x |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源:2011-2012学年安徽省高三第一学期期中考试理科数学 题型:填空题
对于函数① ;②
;② ;③
;③ ;
;
命题甲: 在区间
在区间 上是增函数;
上是增函数;
命题乙: 在区间
在区间 上恰有两个零点
上恰有两个零点 ,且
,且 .
.
能使命题甲、乙均为真命题的函数序号是 .
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
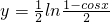 与y=
与y=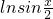 是同一函数;
是同一函数;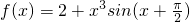 在区间,[-a,a](a>0)上的最大值与最小值的和为4;
在区间,[-a,a](a>0)上的最大值与最小值的和为4;查看答案和解析>>
科目:高中数学 来源:2011-2012学年安徽省六安市舒城中学高三(上)期中数学试卷(理科)(解析版) 题型:填空题
 ,则f(x)=x*lnx的最大值为
,则f(x)=x*lnx的最大值为  -5;②f(x)=|log2x|-
-5;②f(x)=|log2x|- ;③f(x)=cos(x+2)-cosx;
;③f(x)=cos(x+2)-cosx;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com