
【题目】平面上有奇数条线段,甲乙两人做如下游戏:两人轮流(甲先乙后)给任一条尚未设定方向的线段设定一个方向,直至某次(甲)设定后,所有线段各有了一个方向为止.如果最后得到的所有向量之和的模长不小于原来每条线段长,则甲获胜,否则乙获胜.问:谁有必胜策略?证明你的结论.
科目:高中数学 来源: 题型:
【题目】(12分) 由0,1,2,3,4,5这六个数字。
(1)能组成多少个无重复数字的四位数?
(2)能组成多少个无重复数字的四位偶数?
(3)能组成多少个无重复数字且被25个整除的四位数?
(4)组成无重复数字的四位数中比4032大的数有多少个?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某品牌经销商在一广场随机采访男性和女性用户各50名,其中每天玩微信超过6小时的用户列为“微信控”,否则称其为“非微信控”,调查结果如下:
微信控 | 非微信控 | 合计 | |
男性 | 26 | 24 | 50 |
女性 | 30 | 20 | 50 |
合计 | 56 | 44 | 100 |
(1)根据以上数据,能否有95%的把握认为“微信控”与“性别”有关?
(2)现从调查的女性用户中按分层抽样的方法选出5人,求所抽取的5人中“微信控”和“非微信控”的人数;
(3)从(2)中抽取的5位女性中,再随机抽取3人赠送礼品,试求抽取3人中恰有2人位“微信控”的概率.
参考公式: 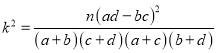 ,其中
,其中![]() .
.
参考数据:
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地政府为科技兴市,欲将如图所示的一块不规则的非农业用地![]() 规划建成一个矩形的高科技工业园区.已知
规划建成一个矩形的高科技工业园区.已知![]() ,
,![]() ,
,![]() ,曲线段
,曲线段![]() 是以点
是以点![]() 为顶点且开口向上的抛物线的一段.如果要使矩形的相邻两边分别落在
为顶点且开口向上的抛物线的一段.如果要使矩形的相邻两边分别落在![]() 、
、![]() 上,且一个顶点
上,且一个顶点![]() 落在曲线段
落在曲线段![]() 上,问应如何规划才能使矩形工业园区的用地面积最大?并求出最大的用地面积(精确到
上,问应如何规划才能使矩形工业园区的用地面积最大?并求出最大的用地面积(精确到![]() ).
).

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有2012位学者参加某数学会议,他们中有些人相互认识,且满足:
(1)每个人至少认识其中的671个人;
(2)对于其中任意两个人![]() 、
、![]() ,若
,若![]() 、
、![]() 相互不认识,则总可以通过其他人间接认识,即存在
相互不认识,则总可以通过其他人间接认识,即存在![]() ,使得
,使得![]() 认识
认识![]() ,
,![]() 认识
认识![]() ,
,![]() 认识
认识![]() ;
;
(3)不可以将2012位学者排成一排,使得相邻的两个人相互认识.
证明:可以将2012位学者分成两组,其中一组能够排成一圈,使得相邻的人相互认识,另一组任何两个人不认识.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() ,
,![]()
(1)当![]() 时,求
时,求![]() 的单调区间;
的单调区间;
(2)①证明:当![]() 时,函数
时,函数![]() 在
在![]() 上恰有一个极值点
上恰有一个极值点![]() ;
;
②求实数![]() 的取值范围,使得对任意的
的取值范围,使得对任意的![]() ,恒有
,恒有![]() 成立.
成立.
注:![]() 为自然对数的底数.
为自然对数的底数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了进一步激发同学们的学习热情,某班级建立了数学英语两个学习兴趣小组,两组的人数如下表所示:
组别 性别 | 数学 | 英语 |
男 | 5 | 1 |
女 | 3 | 3 |
现采用分层抽样的方法(层内采用简单随机抽样)从两组中共抽取3名同学进行测试.
(1)求从数学组抽取的同学中至少有1名女同学的概率;
(2)记ξ为抽取的3名同学中男同学的人数,求随机变量ξ的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com