
【题目】(Ⅰ)解不等式 ![]() >0 (Ⅱ)设a>0,b>0,c>0,且a+b+c=1,求证(
>0 (Ⅱ)设a>0,b>0,c>0,且a+b+c=1,求证( ![]() ﹣1)(
﹣1)( ![]() ﹣1)(
﹣1)( ![]() ﹣1)≥8.
﹣1)≥8.
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,E是PC的中点,求证: (Ⅰ)PA∥平面EDB
(Ⅱ)AD⊥PC.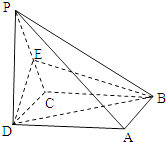
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学高三年级从甲、乙两个班级各选出7名学生参加数学竞赛,他们取得的成绩(满分100分)的茎叶图如图,其中甲班学生的平均分是85,乙班学生成绩的中位数是83. 
(1)求x和y的值;
(2)计算甲班7位学生成绩的方差s2;
(3)从成绩在90分以上的学生中随机抽取两名学生,求甲班至少有一名学生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|2x﹣a|+a.
(1)当a=2时,求不等式f(x)≤6的解集;
(2)设函数g(x)=|2x﹣1|,当x∈R时,f(x)+g(x)≥3,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设F1 , F2分别是椭圆E: ![]() =1(a>b>0)的左、右焦点,过F1倾斜角为45°的直线l与E相交于A,B两点,且|AB|=
=1(a>b>0)的左、右焦点,过F1倾斜角为45°的直线l与E相交于A,B两点,且|AB|= ![]() (Ⅰ)求E的离心率
(Ⅰ)求E的离心率
(Ⅱ)设点P(0,﹣1)满足|PA|=|PB|,求E的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆与双曲线有相同的焦点F1(﹣c,0),F2(c,0),椭圆的一个短轴端点为B,直线F1B与双曲线的一条渐近线平行,若椭圆与双曲线的离心率分别为e1 , e2 , 则3e12+e22的最小值为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平行四边形ABCD中,E,G分别是BC,DC上的点且 ![]() =3
=3 ![]() ,
, ![]() =3
=3 ![]() ,DE与BG交于点O.
,DE与BG交于点O. 
(1)求| ![]() |:|
|:| ![]() |;
|;
(2)若平行四边形ABCD的面积为21,求△BOC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥 ![]() 的底面为正方形,
的底面为正方形, ![]() ⊥底面
⊥底面 ![]() ,则下列结论中不正确的是( )
,则下列结论中不正确的是( )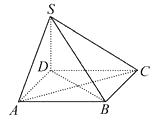
A.![]()
B.![]() ∥平面
∥平面 ![]()
C.![]() 与
与 ![]() 所成的角等于
所成的角等于 ![]() 与
与 ![]() 所成的角
所成的角
D.![]() 与平面
与平面 ![]() 所成的角等于
所成的角等于 ![]() 与平面
与平面 ![]() 所成的角
所成的角
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com