
【题目】如图,PA⊥⊙O所在平面,AB是⊙O的直径,C是⊙O上一点,AE⊥PC,AF⊥PB,给出下列结论:①AE⊥BC;②EF⊥PB;③AF⊥BC;④AE⊥平面PBC,其中真命题的序号是 . 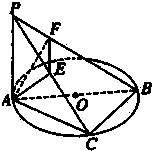
【答案】①②④
【解析】解:①∵AB是⊙O的直径,∴BC⊥AC,∵PA⊥⊙O所在平面,∴PA⊥BC.
又PA∩AC=A,∴BC⊥平面PAC.
∵AE平面PAC.
∴BC⊥AE.
因此①正确.
④由①可知:AE⊥BC,
又∵AE⊥PC,PC∩BC=C,
∴AE⊥平面PBC.
因此④正确.
②由④可知:AE⊥平面PBC,∴AE⊥PB.
又∵AF⊥PB,AE∩AF=A,
∴PB⊥平面AEF,
∴PB⊥EF.
因此②正确.
③AF⊥BC不正确;
用反证法证明:假设AF⊥BC,
又AF⊥PB,PB∩BC=B.
∴AF⊥平面PBC.
这与AE⊥平面PBC相矛盾.因此假设不成立.
故③不正确.
综上可知:只有①②④正确.
所以答案是:①②④.
【考点精析】根据题目的已知条件,利用命题的真假判断与应用的相关知识可以得到问题的答案,需要掌握两个命题互为逆否命题,它们有相同的真假性;两个命题为互逆命题或互否命题,它们的真假性没有关系.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ![]() ,且右准线方程为x=5.
,且右准线方程为x=5.
(1)求椭圆方程;
(2)过椭圆右焦点F作斜率为1的直线l与椭圆C交于A,B两点,P为椭圆上一动点,求△PAB面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】10名工人某天生产同一零件,生产的件数是15,17,14,10,15,17,17,16,14,12,设其平均数为a,中位数为b,众数为c,则有( )
A.a>b>c
B.b>c>a
C.c>a>b
D.c>b>a
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角梯形PBCD中, ![]() ,A为PD的中点,如图.将△PAB沿AB折到△SAB的位置,使SB⊥BC,点E在SD上,且
,A为PD的中点,如图.将△PAB沿AB折到△SAB的位置,使SB⊥BC,点E在SD上,且 ![]() ,如图.
,如图.
(Ⅰ)求证:SA⊥平面ABCD;
(Ⅱ)求二面角E﹣AC﹣D的正切值.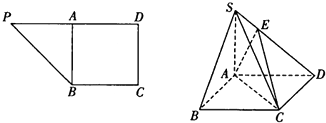
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在菱形ABCD中,∠BAD=60°,线段AD,BD的中点分别为E,F.现将△ABD沿对角线BD翻折,则异面直线BE与CF所成角的取值范围是( ) 
A.( ![]() ,
, ![]() )
)
B.( ![]() ,
, ![]() ]
]
C.( ![]() ,
, ![]() ]
]
D.( ![]() ,
, ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}是等比数列,首项a1=2,a4=16
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)若数列{bn}是等差数列,且b3=a3 , b5=a5 , 求数列{bn}的通项公式及前n项的和.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,过点P(﹣5,a)作圆x2+y2﹣2ax+2y﹣1=0的两条切线,切点分别为M(x1 , y1),N(x2 , y2),且 ![]() +
+ ![]() =0,则实数a的值为 .
=0,则实数a的值为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量 ![]() =(cosωx﹣sinωx,sinωx),
=(cosωx﹣sinωx,sinωx), ![]() =(﹣cosωx﹣sinωx,2
=(﹣cosωx﹣sinωx,2 ![]() cosωx),设函数f(x)=
cosωx),设函数f(x)= ![]() +λ(x∈R)的图象关于直线x=π对称,其中ω,λ为常数,且ω∈(
+λ(x∈R)的图象关于直线x=π对称,其中ω,λ为常数,且ω∈( ![]() ,1)
,1)
(1)求函数f(x)的最小正周期;
(2)若y=f(x)的图象经过点( ![]() ,0)求函数f(x)在区间[0,
,0)求函数f(x)在区间[0, ![]() ]上的取值范围.
]上的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com