
分析 由椭圆及双曲线的定义可知m+n=2a1,m-n=2a2.利用余弦定理,求得10=$\frac{1}{{e}_{1}^{2}}$+$\frac{9}{{e}_{2}^{2}}$,将e2=2e1,即可求得e1.
解答 解:设椭圆与双曲线的半长轴分别为a1,a2,半焦距为c.e1=$\frac{c}{{a}_{1}}$,e2=$\frac{c}{{a}_{2}}$.
设|PF1|=m,|PF2|=n,不妨设m>n,
则m+n=2a1,m-n=2a2.
∴m2+n2=2${a}_{1}^{2}$+2${a}_{2}^{2}$,mn=${a}_{1}^{2}$-${a}_{2}^{2}$
4c2=m2+n2-2mncos∠F1PF2,
∴4c2=2${a}_{1}^{2}$+2${a}_{2}^{2}$-2(${a}_{1}^{2}$-${a}_{2}^{2}$)×$\frac{4}{5}$.
整理得:10c2=${a}_{1}^{2}$+9${a}_{2}^{2}$,
∴10=$\frac{1}{{e}_{1}^{2}}$+$\frac{9}{{e}_{2}^{2}}$,又e2=2e1,
∴40${e}_{1}^{2}$=13,e1∈(0,1).
解得:e1=$\frac{{\sqrt{130}}}{20}$.
∴椭圆的离心率e1=$\frac{{\sqrt{130}}}{20}$.
故答案为:$\frac{{\sqrt{130}}}{20}$.
点评 本题考查双曲线及椭圆的离心率公式,考查余弦定理的应用,考查计算能力,属于中档题.


 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | $\sqrt{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
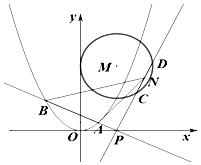 如图,抛物线E:x2=2py(p>0)的焦点为(0,1),圆心M在射线y=2x(x≥0)上且半径为2的圆M与y轴相切.
如图,抛物线E:x2=2py(p>0)的焦点为(0,1),圆心M在射线y=2x(x≥0)上且半径为2的圆M与y轴相切.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | π | B. | $\frac{3π}{4}$ | C. | $\frac{π}{2}$ | D. | $\frac{π}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | d<0 | B. | d>0 | C. | a16<0 | D. | a16>0 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com