练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    设A={x｜–2≤x≤a}，B={y｜y=2x+3，且x∈A}，C={z｜z=x2，且x∈A }，若CB，求实数a的取值范围.

    a的取值范围是(–∞,–2)∪［,3］


    解析:

    ∵y=2x+3在［–2, a］上是增函数

    ∴–1≤y≤2a+3，即B={y｜–1≤y≤2a+3}

    作出z=x2的图像，该函数定义域右端点x=a有三种不同的位置情况如下:

    ①当–2≤a≤0时，a2≤z≤4即C={z｜a2≤z≤4}

    要使CB,必须且只须2a+3≥4得a≥与–2≤a＜0矛盾 

    ②当0≤a≤2时，0≤z≤4即C={z｜0≤z≤4}，要使CB，由图可知:

    必须且只需

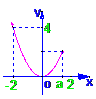
    解得≤a≤2

    ③当a＞2时，0≤z≤a2，即C={z｜0≤z≤a2}，

    要使CB必须且只需

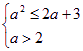    解得2＜a≤3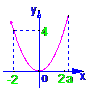

    ④当a＜–2时，A=此时B=C=，则CB成立.

    综上所述，a的取值范围是(–∞,–2)∪［,3］. 

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    设a＞0，a≠1，函数f(x)=a(x2+x+1)有最小值，则不等式loga（x-1）＞0的解集为
    {x|x＞2}
    {x|x＞2}
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    设A={x|x2-2x+a=0}，4∈A，
    （1）求a的值，并写出集合A的所有子集；
    （2）已知B={x|mx+2=0}，若A∪B=A，求m的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    设A={x||x-1|＜2},B={x|＞0},则A∩B等于(    )

    A.{x|-1＜x＜0或2＜x＜3}                    B.{x|x＜0或x＞2}

    C.{x|-1＜x＜3}                                   D.{x|-1＜x＜0}

    查看答案和解析>>

    科目：高中数学 来源： 题型：阅读理解

    仔细阅读下面问题的解法：

        设A=[0, 1],若不等式21-x-a＞0在A上有解,求实数a的取值范围。

        解：由已知可得  a ＜ 21-x

            令f(x)= 21-x ,∵不等式a ＜21-x在A上有解,

            ∴a ＜f(x)在A上的最大值.

            又f(x)在[0,1]上单调递减，f(x)max =f(0)=2.  ∴实数a的取值范围为a＜2.

    研究学习以上问题的解法，请解决下面的问题：

    (1)已知函数f(x)=x2+2x+3(-2≤x≤-1)，求f(x)的反函数及反函数的定义域A；

    (2)对于(1)中的A，设g(x)=，x∈A,试判断g(x)的单调性(写明理由，不必证明)；

    (3)若B ={x|＞2x+a–5}，且对于(1)中的A，A∩B≠F，求实数a的取值范围。

    查看答案和解析>>

    同步练习册答案