
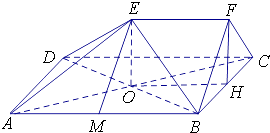
【题目】如图,在五面体ABCDEF中,四边形ABCD是边长为2的正方形,EF∥平面ABCD,EF=1,FB=FC,∠BFC=90°,AE= ![]() .
. 
(1)求证:AB⊥平面BCF;
(2)求直线AE与平面BDE所成角的正切值.
【答案】
(1)证明:取AB的中点M,连接EM,则AM=MB=1,
∵EF∥平面ABCD,EF平面ABEF,平面ABCD∩平面ABEF=AB,
∴EF∥AB,即EF∥MB.
∵EF=MB=1
∴四边形EMBF是平行四边形.
∴EM∥FB,EM=FB.
在Rt△BFC中,FB2+FC2=BC2=4,又FB=FC,得FB= ![]() .
.
∴EM= ![]() .
.
在△AEM中,AE= ![]() ,AM=1,EM=
,AM=1,EM= ![]() ,
,
∴AM2+EM2=3=AE2,
∴AM⊥EM.
∴AM⊥FB,即AB⊥FB.
∵四边形ABCD是正方形,
∴AB⊥BC.
∵FB∩BC=B,FB平面BCF,BC平面BCF,
∴AB⊥平面BCF.
(2)解:连接AC,AC与BD相交于点O,则点O是AC的中点,
取BC的中点H,连接OH,EO,FH,
则OH∥AB,OH= ![]() AB=1.
AB=1.
由(1)知EF∥AB,且EF= ![]() AB,
AB,
∴EF∥OH,且EF=OH.
∴四边形EOHF是平行四边形.
∴E0∥FH,且EO=FH=1.
由(1)知AB⊥平面BCF,又FH平面BCF,
∴FH⊥AB,
∵FH⊥BC,AB∩BC=B,FH平面ABCD,BC平面ABCD,
∴FH⊥平面ABCD.
∴E0⊥平面ABCD.
∵AO平面ABCD,
∴EO⊥AO.
∵AO⊥BD,EO∩BD=O,EO平面EBD,BD平面EBD,
∴AO⊥平面EBD.
∴∠AEO是直线AE与平面BDE所成的角.
在Rt△AOE中,tan∠AEO= ![]() =
= ![]() .
.
∴直线AE与平面BDE所成角的正切值为 ![]() .
.
【解析】(1)先证明出四边形EMBF是平行四边形,推断出EM∥FB,EM=FB.进而在Rt△BFC中求得EM,在△AEM中,根据边长推断出AM2+EM2=3=AE2 , 进而证明出AM⊥EM.然后证明出四边形ABCD是正方形,进而推断出AB⊥BC.最后通过线面垂直的判定定理证明出AB⊥平面BCF.(2)先证明出∠AEO是直线AE与平面BDE所成的角,进而在Rt△AOE中,求得tan∠AEO.
【考点精析】通过灵活运用直线与平面垂直的判定和空间角的异面直线所成的角,掌握一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直;注意点:a)定理中的“两条相交直线”这一条件不可忽视;b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想;已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则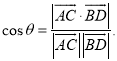 即可以解答此题.
即可以解答此题.


科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,直线PA⊥平面ABCD,AD∥BC,AB⊥AD,BC=2AB=2AD=4BE=4. 
(1)求证:直线DE⊥平面PAC.
(2)若直线PE与平面PAC所成的角的正弦值为 ![]() ,求二面角A﹣PC﹣D的平面角的余弦值.
,求二面角A﹣PC﹣D的平面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x﹣a|. (Ⅰ)若不等式f(x)≤2的解集为[0,4],求实数a的值;
(Ⅱ)在(Ⅰ)的条件下,若x0∈R,使得f(x0)+f(x0+5)﹣m2<4m,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点A(0,0),若函数f(x)的图象上存在两点B、C到点A的距离相等,则称该函数f(x)为“点距函数”,给定下列三个函数:①y=﹣x+2;② ![]() ;③y=x+1.其中,“点距函数”的个数是( )
;③y=x+1.其中,“点距函数”的个数是( )
A.0
B.1
C.2
D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,D为BC的中点,∠BAD+∠C≥90°. (Ⅰ)求证:sin2C≤sin2B;
(Ⅱ)若cos∠BAD=﹣ ![]() ,AB=2,AD=3,求AC.
,AB=2,AD=3,求AC.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com