
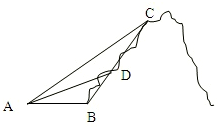
 (2008•奉贤区模拟)如图所示,南山上原有一条笔直的山路BC,现在又新架设了一条索道AC.小李在山脚B处看索道AC,发现张角∠ABC=120°;从B处攀登400米到达D处,回头看索道AC,发现张角∠ADC=160°;从D处再攀登800米方到达C处.问索道AC长多少(精确到米)?
(2008•奉贤区模拟)如图所示,南山上原有一条笔直的山路BC,现在又新架设了一条索道AC.小李在山脚B处看索道AC,发现张角∠ABC=120°;从B处攀登400米到达D处,回头看索道AC,发现张角∠ADC=160°;从D处再攀登800米方到达C处.问索道AC长多少(精确到米)?| BD |
| sin∠DAB |
| AD |
| sin∠ABD |
 解:在△ABC中,BD=400,∠ABD=120°,
解:在△ABC中,BD=400,∠ABD=120°,| BD |
| sin∠DAB |
| AD |
| sin∠ABD |
| 400 |
| sin40° |
| AD |
| sin120° |


科目:高中数学 来源: 题型:
| x+y |
| 2 |
| x+y |
| 2 |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
. |
| x\~(a1)(a2)(a3)…(an-1)(an) |
. |
| 2\~(-1)(3)(-2)(1) |
| 1 |
| 1-ak |
. |
| 2\~(a1)(a2)(a3)…(a3n-2)(a3n-1)(a3n) |
| 2 |
| 7 |
| 2 |
| 7 |
. | ||||||||||
t\~(
|
| lim |
| n→∞ |
| dn |
| dn+1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com