
【题目】![]() 指数是用体重公斤数除以身高米数的平方得出的数字,是国际上常用的衡量人体胖瘦程度以及是否健康的一个标准.对于高中男体育特长生而言,当BMI数值大于或等于20.5时,我们说体重较重;当
指数是用体重公斤数除以身高米数的平方得出的数字,是国际上常用的衡量人体胖瘦程度以及是否健康的一个标准.对于高中男体育特长生而言,当BMI数值大于或等于20.5时,我们说体重较重;当![]() 数值小于20.5时,我们说体重较轻;身高大于或等于170
数值小于20.5时,我们说体重较轻;身高大于或等于170![]() 的我们说身高较高;身高小于170
的我们说身高较高;身高小于170![]() 的我们说身高较矮.
的我们说身高较矮.
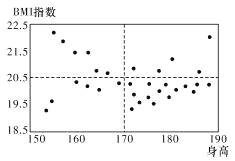
(1)已知某高中共有32名男体育特长生,其身高与![]() 指数的数据如散点图所示,请根据所得信息,完成下列列联表,并判断是否有95%的把握认为男体育特长生的身高对
指数的数据如散点图所示,请根据所得信息,完成下列列联表,并判断是否有95%的把握认为男体育特长生的身高对![]() 指数有影响;
指数有影响;
身高较矮 | 身高较高 | 合计 | |
体重较轻 | |||
体重较重 | |||
合计 |
(2)①从上述32名男体育特长生中随机选取8名,其身高和体重的数据如下表所示:
编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
身高 | 166 | 167 | 160 | 173 | 178 | 169 | 158 | 173 |
体重 | 57 | 58 | 53 | 61 | 66 | 57 | 50 | 66 |
根据最小二乘法的思想与公式求得线性回归方程为![]() .利用已经求得的线性回归方程,请完善下列残差表,并求解释变量(身高)对于预报变量(体重)变化的贡献率
.利用已经求得的线性回归方程,请完善下列残差表,并求解释变量(身高)对于预报变量(体重)变化的贡献率![]() (保留两位有效数字);
(保留两位有效数字);
编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
体重 | 57 | 58 | 53 | 61 | 66 | 57 | 50 | 66 |
残差 | 0.1 | 0.3 | 0.9 | -1.5 | -0.5 |
②通过残差分析,对于残差(绝对值)最大的那组数据,需要确认在样本点的采集中是否有人为的错误.已知通过重新采集发现,该组数据的体重应该为58(kg).请重新根据最小二乘法的思想与公式,求出男体育特长生的身高与体重的线性回归方程.
(参考公式)
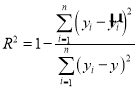 ,
,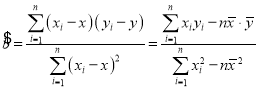 ,
,
![]() ,
,![]() ,
,
 (
(![]() ).
).
| 0.10 | 0.05 | 0.01 | 0.005 |
| 2.706 | 3.841 | 6.635 | 7.879 |
(参考数据)
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() .
.
【答案】(1)见解析,没有(2)①见解析,![]() 约为0.91②
约为0.91②![]()
【解析】
(1)根据散点图即可完成列联表;套用公式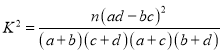 (
(![]() ),算出观测值,与3.841作比较,即可得到本题答案;
),算出观测值,与3.841作比较,即可得到本题答案;
(2)①把![]() 分别代入
分别代入![]() ,即可完善下列残差表;然后套用公式
,即可完善下列残差表;然后套用公式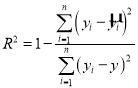 ,即可得到本题答案;
,即可得到本题答案;
②由①可知,第八组数据的体重应为58,套用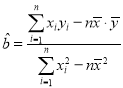 ,
,![]() ,即可得到本题答案.
,即可得到本题答案.
(1)
身高较矮 | 身高较高 | 合计 | |
体重较轻 | 6 | 15 | 21 |
体重较重 | 6 | 5 | 11 |
合计 | 12 | 20 | 32 |
由于![]()
因此没有![]() 的把握认为男体育特长生的身高对
的把握认为男体育特长生的身高对![]() 指数有影响.
指数有影响.
(2)①
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
体重 | 57 | 58 | 53 | 61 | 66 | 57 | 50 | 66 |
残差 | 0.1 | 0.3 | 0.9 | -1.5 | -0.5 | -2.3 | -0.5 | 3.5 |
![]()
 ,
,
所以解释变量(身高)对于预报变量(体重)变化的贡献率![]() 约为0.91.
约为0.91.
②由①可知,第八组数据的体重应为58.
此时![]() ,
,
又![]() ,
,![]() ,
,![]() ,
,
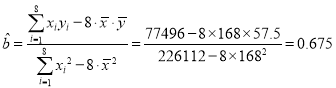 ,
,![]() ,
,
所以重新采集数据后,男体育特长生的身高与体重的线性回归方程为![]() .
.


 计算高手系列答案
计算高手系列答案科目:高中数学 来源: 题型:
【题目】2019年上半年我国多个省市暴发了“非洲猪瘟”疫情,生猪大量病死,存栏量急剧下降,一时间猪肉价格暴涨,其他肉类价格也跟着大幅上扬,严重影响了居民的生活.为了解决这个问题,我国政府一方面鼓励有条件的企业和散户防控疫情,扩大生产;另一方面积极向多个国家开放猪肉进口,扩大肉源,确保市场供给稳定.某大型生猪生产企业分析当前市场形势,决定响应政府号召,扩大生产决策层调阅了该企业过去生产相关数据,就“一天中一头猪的平均成本与生猪存栏数量之间的关系”进行研究.现相关数据统计如下表:
生猪存栏数量 | 2 | 3 | 4 | 5 | 8 |
头猪每天平均成本 | 3.2 | 2.4 | 2 | 1.9 | 1.5 |
(1)研究员甲根据以上数据认为![]() 与
与![]() 具有线性回归关系,请帮他求出
具有线性回归关系,请帮他求出![]() 关于
关于![]() 的线.性回归方程
的线.性回归方程![]() (保留小数点后两位有效数字)
(保留小数点后两位有效数字)
(2)研究员乙根据以上数据得出![]() 与
与![]() 的回归模型:
的回归模型:![]() .为了评价两种模型的拟合效果,请完成以下任务:
.为了评价两种模型的拟合效果,请完成以下任务:
①完成下表(计算结果精确到0.01元)(备注:![]() 称为相应于点
称为相应于点![]() 的残差);
的残差);
生猪存栏数量 | 2 | 3 | 4 | 5 | 8 | |
头猪每天平均成本 | 3.2 | 2.4 | 2 | 1.9 | 1.5 | |
模型甲 | 估计值 | |||||
残差 | ||||||
模型乙 | 估计值 | 3.2 | 2.4 | 2 | 1.76 | 1.4 |
残差 | 0 | 0 | 0 | 0.14 | 0.1 | |
②分别计算模型甲与模型乙的残差平方和![]() 及
及![]() ,并通过比较
,并通过比较![]() 的大小,判断哪个模型拟合效果更好.
的大小,判断哪个模型拟合效果更好.
(3)根据市场调查,生猪存栏数量达到1万头时,饲养一头猪每一天的平均收入为7.5元;生猪存栏数量达到1.2万头时,饲养一头猪每一天的平均收入为7.2元若按(2)中拟合效果较好的模型计算一天中一头猪的平均成本,问该生猪存栏数量选择1万头还是1.2万头能获得更多利润?请说明理由.(利润=收入-成本)
参考公式: .
.
参考数据:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,直四棱柱ABCD–A1B1C1D1的底面是菱形,AA1=4,AB=2,∠BAD=60°,E,M,N分别是BC,BB1,A1D的中点.
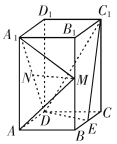
(1)证明:MN∥平面C1DE;
(2)求点C到平面C1DE的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)求函数![]() 的极值;
的极值;
(2)对于曲线上的不同两点![]() ,如果存在曲线上的点
,如果存在曲线上的点![]() ,且
,且![]() 使得曲线在点
使得曲线在点![]() 处的切线
处的切线![]() ,则称
,则称![]() 为弦
为弦![]() 的伴随直线,特别地,当
的伴随直线,特别地,当![]() 时,又称
时,又称![]() 为
为![]() 的
的![]() —伴随直线.
—伴随直线.
①求证:曲线![]() 的任意一条弦均有伴随直线,并且伴随直线是唯一的;
的任意一条弦均有伴随直线,并且伴随直线是唯一的;
②是否存在曲线![]() ,使得曲线
,使得曲线![]() 的任意一条弦均有
的任意一条弦均有![]() —伴随直线?若存在,给出一条这样的曲线,并证明你的结论;若不存在,说明理由.
—伴随直线?若存在,给出一条这样的曲线,并证明你的结论;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy下,曲线C1的参数方程为![]() (
(![]() 为参数),曲线C1在变换T:
为参数),曲线C1在变换T:![]() 的作用下变成曲线C2.
的作用下变成曲线C2.
(1)求曲线C2的普通方程;
(2)若m>1,求曲线C2与曲线C3:y=m|x|-m的公共点的个数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以原点
为参数),以原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的极坐标方程及
的极坐标方程及![]() 的直角坐标方程;
的直角坐标方程;
(2)设![]() 与曲线
与曲线![]() 、
、![]() 分别交于异于原点的点
分别交于异于原点的点![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C过点M(1,![]() ),两个焦点为A(﹣1,0),B(1,0),O为坐标原点.
),两个焦点为A(﹣1,0),B(1,0),O为坐标原点.
(1)求椭圆C的方程;
(2)直线l过点A(﹣1,0),且与椭圆C交于P,Q两点,求△BPQ面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com