
����Ŀ�������ͣ���̵��С�����������ÿ���˶�Ӧ��Ҳ�������صĽ�ͨ������һ���˾���·����������ͨ�źŵơ�����н���·�ڵġ��й�ʽ����·���������������Ҵ��ںܴ�Ľ�ͨ��ȫ������һ�������Ƿ���ڡ��й�ʽ����·���Ǻ����������������̶ȵ���Ҫָ�꣮ij�������Ϊ���˽�·�˶ԡ��й�ʽ����·����̬�ȣ�����·�������ȡ30��·�˽������ʾ����飬�õ���������������
���� | Ů�� | �ϼ� | |
���� | 10 | ||
������ | 8 | ||
�ϼ� | 30 |
��֪����30���������ȡ1�˳鵽���С��й�ʽ����·����·�˵ĸ�����![]() ��
��
��1���뽫����������������������ڴ������ֱ����д���������Ҫд�����̣������ݴ������������ж��Ƿ���95%�İ�����Ϊ���С��й�ʽ����·�����Ա��йأ�
��2��������30���е�Ů��·���������ȡ2�˲μ�һ�����Ƿ��С��й�ʽ����·��������ΪX����X�ķֲ��м�����ѧ������
����![]() ������n=a+b+c+d
������n=a+b+c+d
P��K2��k0�� | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
���𰸡�(1)��������(2)������
��������
��1������������������![]() �Ĺ۲�ֵ
�Ĺ۲�ֵ![]() �����ݽ����жϼ��ɣ�
�����ݽ����жϼ��ɣ�
��2���ֱ����X=0��1��2��Ӧ�ĸ��ʣ��г�X�ķֲ��������ѧ�������ɣ�
��1���������������£�
���� | Ů�� | �ϼ� | |
���� | 10 | 6 | 16 |
������ | 6 | 8 | 14 |
�ϼ� | 16 | 14 | 30 |
�����������������ɹ�ʽ����ã�
![]() �Ĺ۲�ֵ
�Ĺ۲�ֵ![]() =
=![]() ��1.158��3.841��
��1.158��3.841��
��û��95%�İ�����Ϊ���С��й�ʽ����·�����Ա��йأ�
��2��X�Ŀ���ȡֵΪ0��1��2��
![]() ��
��![]() ��
��![]() ��
��
��X�ķֲ����ǣ�
X | 0 | 1 | 2 |
P |
|
|
|
��E��X��=0��![]() +1��
+1��![]() +2��
+2��![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��[ѡ��4-5������ʽѡ��]
��֪����f��x��=|x+1|��|x��2|��
��1����ʽf��x����1�Ľ⼯��
��2��������ʽf��x����x2��x+m�Ľ⼯�ǿգ���m��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����A��0��2����ֱ��![]() ����ԲC��
����ԲC��![]() ����P��Q���㣮
����P��Q���㣮
��1����ֱ��![]() ��б��Ϊk����k��ȡֵ��Χ��
��б��Ϊk����k��ȡֵ��Χ��
��2������PQΪֱ����Բ������E��1��0������ֱ��![]() �ķ��̣�
�ķ��̣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ������£��������ɵ��ϵij����ٶ� ![]() ����λ��ǧ��/Сʱ���dz����ܶ�
����λ��ǧ��/Сʱ���dz����ܶ� ![]() ����λ����/ǧ�ף��ĺ����������ɵ��ϵij����ܶȴﵽ200��/ǧ��ʱ����ɶ�������ʱ�����ٶ�Ϊ0ǧ��/Сʱ���������ܶȲ�����20��/ǧ��ʱ�������ٶ�Ϊ60ǧ��/Сʱ���о���������
����λ����/ǧ�ף��ĺ����������ɵ��ϵij����ܶȴﵽ200��/ǧ��ʱ����ɶ�������ʱ�����ٶ�Ϊ0ǧ��/Сʱ���������ܶȲ�����20��/ǧ��ʱ�������ٶ�Ϊ60ǧ��/Сʱ���о��������� ![]() ʱ�������ٶ�
ʱ�������ٶ� ![]() �dz����ܶ�
�dz����ܶ� ![]() ��һ�κ�����
��һ�κ�����
��1���� ![]() ʱ������
ʱ������ ![]() �ı���ʽ��
�ı���ʽ��
��2���������ܶ�Ϊ���ʱ������������λʱ����ͨ�����ɵ���ij�۲��ij���������λ����/Сʱ�� ![]() ���Դﵽ���������ֵ������ȷ��1��/Сʱ��
���Դﵽ���������ֵ������ȷ��1��/Сʱ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ȱ�����{an}�У���������am��anʹ��![]() =4a1 �� ��a6=a5+2a4 �� ��
=4a1 �� ��a6=a5+2a4 �� ��![]() ����Сֵ�ǣ�������
����Сֵ�ǣ�������
A.![]()
B.2
C.![]()
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������Բ![]() ��a��2����������Ϊ
��a��2����������Ϊ![]() ��б��Ϊk��k��0����ֱ��L����E��0��1��������Բ����C��D���㣮
��б��Ϊk��k��0����ֱ��L����E��0��1��������Բ����C��D���㣮
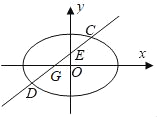
��������Բ�ı����̣�
������ֱ��l��x���ཻ�ڵ�G����![]() ����k��ֵ��
����k��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������� ![]() ��ͼ������ƽ��m��m��0������λ���Ⱥ����õ���ͼ�����y��Գƣ���m����Сֵ�ǣ� ��
��ͼ������ƽ��m��m��0������λ���Ⱥ����õ���ͼ�����y��Գƣ���m����Сֵ�ǣ� ��
A.![]()
B.![]()
C.![]()
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ԲC�� ![]() (a>b>0)��һ������ΪA(2,0)��������Ϊ
(a>b>0)��һ������ΪA(2,0)��������Ϊ![]() .ֱ��y��k(x��1)����ԲC���ڲ�ͬ������M��N.
.ֱ��y��k(x��1)����ԲC���ڲ�ͬ������M��N.
(1)����ԲC�ķ��̣�
(2)����AMN�����Ϊ![]() ʱ����k��ֵ��
ʱ����k��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij������7ʱ�˴�������������![]() ����/Сʱ
����/Сʱ![]() ��
��![]() ��ǰ�����50�����
��ǰ�����50�����![]() �ۣ�Ȼ�������������
�ۣ�Ȼ�������������![]() ǧ��/Сʱ(
ǧ��/Сʱ(![]() )��
)��![]() ��ǰ�����
��ǰ�����![]() ǧ��
ǧ��![]() �У��ƻ���������4��9ʱ����
�У��ƻ���������4��9ʱ����![]() ��.��˴�����������Ҫ��ʱ��ֱ�Ϊ
��.��˴�����������Ҫ��ʱ��ֱ�Ϊ![]() ��
��![]() Сʱ���������Ҫ�ľ���
Сʱ���������Ҫ�ľ���![]() (��λ��Ԫ)
(��λ��Ԫ)

(1)���ú���![]() ��
��![]() �Ĵ���ʽ��ʾ
�Ĵ���ʽ��ʾ![]() ��
��
(2)Ҫʹ�����辭��![]() ���٣���
���٣���![]() ��
��![]() ��ֵ���������ʱ�ķ���.
��ֵ���������ʱ�ķ���.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com