
【题目】若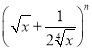 展开式中前三项系数成等差数列,求:
展开式中前三项系数成等差数列,求:
(1)展开式中含x的一次幂的项;
(2)展开式中所有x 的有理项;
(3)展开式中系数最大的项。
科目:高中数学 来源: 题型:
【题目】如图,小明从街道的E处出发,先到F处与小红会合,再一起到位于G处的老年公寓参加志愿者活动,则小明到老年公寓可以选择的最短路径条数为( )

A. 9B. 12C. 18D. 24
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知指数函数![]() 满足:
满足:![]() ,定义域为
,定义域为![]() 的函数
的函数![]() 是奇函数.
是奇函数.
(1)求![]() 的值;
的值;
(2)判断函数![]() 的单调性并用定义加以证明;
的单调性并用定义加以证明;
(3)若对任意的 ![]() ,不等式
,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABC﹣A1B1C1中,∠ACB=90°,AC=BC=2,D,E分别为棱AB,BC的中点,M为棱AA1的中点.

(1)证明:A1B1⊥C1D;
(2)若AA1=4,求三棱锥A﹣MDE的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
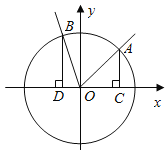
【题目】(本小题满分13分)如图,在直角坐标系![]() 中,角
中,角![]() 的顶点是原点,始边与
的顶点是原点,始边与![]() 轴正半轴重合.终边交单位圆于点
轴正半轴重合.终边交单位圆于点![]() ,且
,且![]() ,将角
,将角![]() 的终边按逆时针方向旋转
的终边按逆时针方向旋转![]() ,交单位圆于点
,交单位圆于点![]() ,记
,记![]() .
.
(1)若![]() ,求
,求![]() ;
;
(2)分别过![]() 作
作![]() 轴的垂线,垂足依次为
轴的垂线,垂足依次为![]() ,记
,记![]() 的面积为
的面积为![]() ,
,![]() 的面积为
的面积为![]() ,若
,若![]() ,求角
,求角![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知平面内两点![]() .
.
(1)求![]() 的中垂线方程;
的中垂线方程;
(2)求过![]() 点且与直线
点且与直线![]() 平行的直线
平行的直线![]() 的方程;
的方程;
(3)一束光线从![]() 点射向(2)中的直线
点射向(2)中的直线![]() ,若反射光线过点
,若反射光线过点![]() ,求反射光线所在的直线方程.
,求反射光线所在的直线方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于![]() 的方程
的方程![]() ,给出下列四个命题
,给出下列四个命题
①存在实数![]() ,使得方程恰有2个不同的实根;
,使得方程恰有2个不同的实根;
②存在实数![]() ,使得方程恰有4个不同的实根;
,使得方程恰有4个不同的实根;
③存在实数![]() ,使得方程恰有5个不同的实根;
,使得方程恰有5个不同的实根;
④存在实数![]() ,使得方程恰有7个不同的实根
,使得方程恰有7个不同的实根
A.3B.2C.1D.0
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某车间生产某种电子元件,如果生产出一件正品,可获利200元,如果生产出一件次品,则损失100元.已知该车间制造电子元件的过程中,次品率![]() 与日产量
与日产量![]() 的函数关系是:
的函数关系是:![]() .
.
(1)写出该车间的日盈利额![]() (元)与日产量
(元)与日产量![]() (件)之间的函数关系式;
(件)之间的函数关系式;
(2)为使日盈利额最大,该车间的日产量应定为多少件?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com