
【题目】如图,直三棱柱![]() 中,
中,![]() 分别是
分别是![]() 的中点,
的中点,![]() .
.
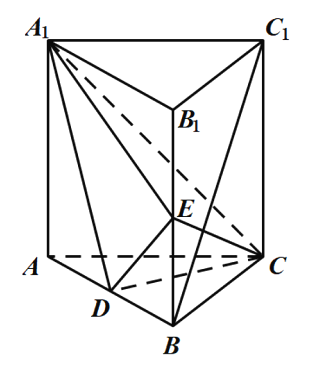
(1)证明:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知数列![]() ,
,![]() 满足
满足![]() (
(![]() …).
…).
(1)若![]() ,求
,求![]() 的值;
的值;
(2)若![]() 且
且![]() ,则数列
,则数列![]() 中第几项最小?请说明理由;
中第几项最小?请说明理由;
(3)若![]() (n=1,2,3,…),求证:“数列
(n=1,2,3,…),求证:“数列![]() 为等差数列”的充分必要条件是“数列
为等差数列”的充分必要条件是“数列![]() 为等差数列且
为等差数列且![]() (n=1,2,3,…)”.
(n=1,2,3,…)”.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,且与双曲线
,且与双曲线![]() 有相同的焦点.
有相同的焦点.
(1)求椭圆![]() 的方程;
的方程;
(2)直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() ,
,![]() 两点,点
两点,点![]() 满足
满足![]() ,点
,点![]() ,若直线
,若直线![]() 斜率为
斜率为![]() ,求
,求![]() 面积的最大值及此时直线
面积的最大值及此时直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() 为常数) .
为常数) .
(1)当![]() 时,求曲线
时,求曲线![]() 在
在![]() 处的切线方程:
处的切线方程:
(2)若函数![]() 在
在![]() 内存在唯一极值点
内存在唯一极值点![]() ,求实数
,求实数![]() 的取值范围,并判断
的取值范围,并判断![]() ,是
,是![]() 在
在![]() 内的极大值点还是极小值点.
内的极大值点还是极小值点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 的两个焦点与短轴的一个端点是直角三角形的三个顶点,直线
的两个焦点与短轴的一个端点是直角三角形的三个顶点,直线![]() :
: ![]() 与椭圆
与椭圆![]() 有且只有一个公共点.
有且只有一个公共点.
(Ⅰ)求椭圆![]() 的方程及点
的方程及点![]() 的坐标;
的坐标;
(Ⅱ)设![]() 是坐标原点,直线
是坐标原点,直线![]() 平行于
平行于![]() ,与椭圆
,与椭圆![]() 交于不同的两点
交于不同的两点![]() 、
、![]() ,且与直线
,且与直线![]() 交于点
交于点![]() ,证明:存在常数
,证明:存在常数![]() ,使得
,使得![]() ,并求
,并求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() (
(![]() )的焦距为4,其短轴的两个端点与长轴的一个端点构成正三角形.
)的焦距为4,其短轴的两个端点与长轴的一个端点构成正三角形.
(1)求椭圆C的标准方程;
(2)设F为椭圆C的左焦点,T为直线![]() 上任意一点,过F作TF的垂线交椭圆C于点P,Q.
上任意一点,过F作TF的垂线交椭圆C于点P,Q.
(i)证明:OT平分线段PQ(其中O为坐标原点);
(ii)当![]() 最小时,求点T的坐标.
最小时,求点T的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知椭圆![]()
![]() 过点
过点![]() 两个焦点为
两个焦点为![]() 和
和![]() .圆O的方程为
.圆O的方程为![]() .
.
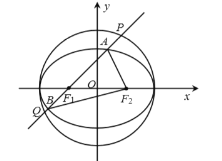
(1)求椭圆C的标准方程;
(2)过![]() 且斜率为
且斜率为![]() 的动直线l与椭圆C交于A、B两点,与圆O交于P、Q两点(点A、P在x轴上方),当
的动直线l与椭圆C交于A、B两点,与圆O交于P、Q两点(点A、P在x轴上方),当![]()
![]()
![]() 成等差数列时,求弦PQ的长.
成等差数列时,求弦PQ的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】大数据时代对于现代人的数据分析能力要求越来越高,数据拟合是一种把现有数据通过数学方法来代入某条数式的表示方式,比如![]() ,
,![]()
![]() ,2,
,2,![]() ,n是平面直角坐标系上的一系列点,用函数
,n是平面直角坐标系上的一系列点,用函数![]() 来拟合该组数据,尽可能使得函数图象与点列
来拟合该组数据,尽可能使得函数图象与点列![]() 比较接近.其中一种描述接近程度的指标是函数的拟合误差,拟合误差越小越好,定义函数
比较接近.其中一种描述接近程度的指标是函数的拟合误差,拟合误差越小越好,定义函数![]() 的拟合误差为:
的拟合误差为:![]() .已知平面直角坐标系上5个点的坐标数据如表:
.已知平面直角坐标系上5个点的坐标数据如表:
x | 1 | 3 | 5 | 7 | 9 |
y | 12 |
| 4 |
| 12 |
![]() 若用一次函数
若用一次函数![]() 来拟合上述表格中的数据,求该函数的拟合误差
来拟合上述表格中的数据,求该函数的拟合误差![]() 的最小值,并求出此时的函数解析式
的最小值,并求出此时的函数解析式![]() ;
;
![]() 若用二次函数
若用二次函数![]() 来拟合题干表格中的数据,求
来拟合题干表格中的数据,求![]() ;
;
![]() 请比较第
请比较第![]() 问中的
问中的![]() 和第
和第![]() 问中的
问中的![]() ,用哪一个函数拟合题目中给出的数据更好?
,用哪一个函数拟合题目中给出的数据更好?![]() 请至少写出三条理由
请至少写出三条理由![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是边长为
是边长为![]() 的菱形,
的菱形,![]() ,
, ![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() 为
为![]() 的中点.
的中点.
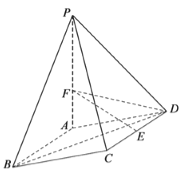
(1)求证:![]() ;
;
(2)求异面直线![]() 与
与![]() 所成角的余弦值;
所成角的余弦值;
(3)判断直线![]() 与平面
与平面![]() 的位置关系,请说明理由.
的位置关系,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com