
下列结论正确的是( )
A.当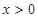 且 且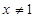 时, 时,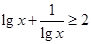 ; ; | B.当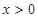 时, 时,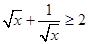 ; ; |
C.当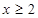 时, 时,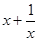 的最小值为2; 的最小值为2; | D.当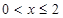 时, 时,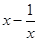 无最大值; 无最大值; |
科目:高中数学 来源: 题型:单选题
在实数集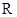 中定义一种运算“
中定义一种运算“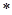 ”,对任意
”,对任意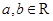 ,
,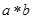 为唯一确定的实数,且具有性质:
为唯一确定的实数,且具有性质:
(1)对任意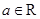 ,
,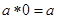 ;
;
(2)对任意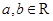 ,
,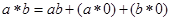 .
.
则函数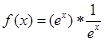 的最小值为( )
的最小值为( )
A. | B. | C.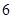 | D.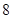 |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
设椭圆 +
+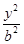 =1和x轴正半轴交点为A,和y轴正半轴的交点为B,P为第一象限内椭圆上的点,那么四边形OAPB面积最大值为( )
=1和x轴正半轴交点为A,和y轴正半轴的交点为B,P为第一象限内椭圆上的点,那么四边形OAPB面积最大值为( )
A. ab ab | B. ab ab | C. ab ab | D.2ab |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com