
【题目】有一个不透明的袋子,装有4个大小形状完全相同的小球,球上分别标有数字1,2,3,4.现按如下两种方式随机取球两次,每种方式中第1次取到球的编号记为![]() ,第2次取到球的编号记为
,第2次取到球的编号记为![]() .
.
(1)若逐个不放回地取球,求![]() 是奇数的概率;
是奇数的概率;
(2)若第1次取完球后将球再放回袋中,然后进行第2次取球,求直线![]() 与双曲线
与双曲线![]() 有公共点的概率.
有公共点的概率.
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案科目:高中数学 来源: 题型:
【题目】2019年4月,甲乙两校的学生参加了某考试机构举行的大联考,现对这两校参加考试的学生的数学成绩进行统计分析,数据统计显示,考生的数学成绩![]() 服从正态分布
服从正态分布![]() ,从甲乙两校100分及以上的试卷中用系统抽样的方法各抽取了20份试卷,并将这40份试卷的得分制作成如图所示的茎叶图:
,从甲乙两校100分及以上的试卷中用系统抽样的方法各抽取了20份试卷,并将这40份试卷的得分制作成如图所示的茎叶图:
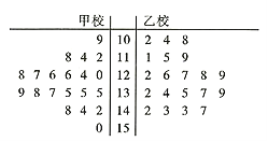
(1)试通过茎叶图比较这40份试卷的两校学生数学成绩的中位数;
(2)若把数学成绩不低于135分的记作数学成绩优秀,根据茎叶图中的数据,判断是否有![]() 的把握认为数学成绩在100分及以上的学生中数学成绩是否优秀与所在学校有关?
的把握认为数学成绩在100分及以上的学生中数学成绩是否优秀与所在学校有关?
(3)从所有参加此次联考的学生中(人数很多)任意抽取3人,记数学成绩在134分以上的人数为![]() ,求
,求![]() 的数学期望.
的数学期望.
附:若随机变量![]() 服从正态分布
服从正态分布![]() ,则
,则![]() ,
,![]()
![]() ,
,![]() .
.
参考公式与临界值表:![]() ,其中
,其中![]() .
.
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】博览会安排了分别标有序号为“1号”“2号”“3号”的三辆车,等可能随机顺序前往酒店接嘉宾.某嘉宾突发奇想,设计两种乘车方案.方案一:不乘坐第一辆车,若第二辆车的车序号大于第一辆车的车序号,就乘坐此车,否则乘坐第三辆车;方案二:直接乘坐第一辆车.记方案一与方案二坐到“3号”车的概率分别为P1,P2,则( )
A. P1P2=![]() B. P1=P2=
B. P1=P2=![]() C. P1+P2=
C. P1+P2=![]() D. P1<P2
D. P1<P2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某幼儿园举办“yue”主题系列活动——“悦”动越健康亲子运动打卡活动,为了解小朋友坚持打卡的情况,对该幼儿园所有小朋友进行了调查,调查结果如下表:
打卡天数 | 17 | 18 | 19 | 20 | 21 |
男生人数 | 3 | 5 | 3 | 7 | 2 |
女生人数 | 3 | 5 | 5 | 7 | 3 |
(1)根据上表数据,求该幼儿园男生平均打卡的天数;
(2)若从打卡21天的小朋友中任选2人交流心得,求选到男生和女生各1人的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂预购软件服务,有如下两种方案:
方案一:软件服务公司每日收取工厂60元,对于提供的软件服务每次10元;
方案二:软件服务公司每日收取工厂200元,若每日软件服务不超过15次,不另外收费,若超过15次,超过部分的软件服务每次收费标准为20元.
(1)设日收费为![]() 元,每天软件服务的次数为
元,每天软件服务的次数为![]() ,试写出两种方案中
,试写出两种方案中![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)该工厂对过去100天的软件服务的次数进行了统计,得到如图所示的条形图,依据该统计数据,把频率视为概率,从节约成本的角度考虑,从两个方案中选择一个,哪个方案更合适?请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com