
【题目】已知椭圆C: ![]() 的一个焦点与抛物线y2=-4x的焦点相同,且椭圆C上一点与椭圆C的左,右焦点F1,F2构成的三角形的周长为
的一个焦点与抛物线y2=-4x的焦点相同,且椭圆C上一点与椭圆C的左,右焦点F1,F2构成的三角形的周长为![]() .
.
(1)求椭圆C的方程;
(2)若直线l:y=kx+m(k,m∈R)与椭圆C交于A,B两点,O为坐标原点,△AOB的重心G满足: ![]() ,求实数m的取值范围.
,求实数m的取值范围.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】试题分析:(1)利用与抛物线有公共焦点、椭圆的定义及几何要素间的等量关系进行求解;(2)联立直线和椭圆的方程,得到关于![]() 的一元二次方程,利用根与系数的关系、三角形的重心性质和平面向量的数量积运算进行求解.
的一元二次方程,利用根与系数的关系、三角形的重心性质和平面向量的数量积运算进行求解.
试题解析:(1)依题意得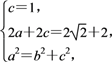
即![]()
所以椭圆C的方程为![]() +y2=1.
+y2=1.
(2)设A(x1,y1),B(x2,y2),
联立得方程组![]()
消去y并整理得(1+2k2)x2+4kmx+2m2-2=0,
则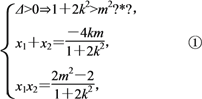
设△AOB的重心为G(x,y),
由![]() ·
·![]() =-
=-![]() ,
,
可得x2+y2=![]() .②
.②
由重心公式可得G(![]() ,
,![]() ),
),
代入②式,整理可得(x1+x2)2+(y1+y2)2=4(x1+x2)2+[k(x1+x2)+2m]2=4,③
将①式代入③式并整理,
得m2=![]() ,
,
代入(*)得k≠0,
则m2=![]() =1+
=1+![]() =1+
=1+![]() .
.
∵k≠0,∴t=![]() >0,∴t2+4t>0,
>0,∴t2+4t>0,
∴m2>1,∴m∈(-∞,-1)∪(1,+∞).


 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案科目:高中数学 来源: 题型:
【题目】某化工厂引进一条先进生产线生产某种化工产品,其生产的总成本![]() (万元)与年产量
(万元)与年产量![]() (吨)之间的函数关系式可以近似的表示为
(吨)之间的函数关系式可以近似的表示为![]() ,已知此生产线年产量最大为
,已知此生产线年产量最大为![]() 吨.
吨.
(1)求年产量为多少吨时,生产每吨产品的平均成本最低,并求最低成本;
(2)若每吨产品平均出厂价为40万元,那么当年产量为多少吨时,可以获得最大利润?最大利润是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,将曲线
中,将曲线![]() 上的所有点横坐标伸长为原来的
上的所有点横坐标伸长为原来的![]() 倍,纵坐标伸长为原来的2倍后,得到曲线
倍,纵坐标伸长为原来的2倍后,得到曲线![]() ,在以
,在以![]() 为极点,
为极点, ![]() 轴正半轴为极轴的极坐标系中,直线
轴正半轴为极轴的极坐标系中,直线![]() 的极坐标方程是
的极坐标方程是![]() .
.
(1)写出曲线![]() 的参数方程和直线
的参数方程和直线![]() 的直角坐标方程;
的直角坐标方程;
(2)在曲线![]() 上求一点
上求一点![]() ,使点
,使点![]() 到直线
到直线![]() 的距离
的距离![]() 最大,并求出此最大值.
最大,并求出此最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() 的左焦点为F(-1,0),经过点F的直线l0与椭圆交于A,B两点.当直线l0⊥x轴时,|AB|=
的左焦点为F(-1,0),经过点F的直线l0与椭圆交于A,B两点.当直线l0⊥x轴时,|AB|=![]() .
.
(1)求椭圆C的方程;
(2)作直线l⊥x轴,分别过A,B作AA1⊥l,垂足为A1,BB1⊥l,垂足为B1,且△A1FB1是直角三角形.问:是否存在直线l使得∠A1FO=2∠B1FO?若存在,求出直线l的方程;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,C1的参数方程为 (t为参数),在以坐标原点为极点,x轴正半轴为极轴的极坐标系中,C2的极坐标方程ρ2-2ρcos θ-3=0.
(t为参数),在以坐标原点为极点,x轴正半轴为极轴的极坐标系中,C2的极坐标方程ρ2-2ρcos θ-3=0.
(Ⅰ)说明C2是哪种曲线,并将C2的方程化为普通方程;
(Ⅱ)C1与C2有两个公共点A,B,定点P的极坐标![]() ,求线段AB的长及定点P到A,B两点的距离之积.
,求线段AB的长及定点P到A,B两点的距离之积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{an}的首项a1=1,公差d>0.且a2,a5,a14分别是等比数列{bn}的b2,b3,b4.
(1)求数列{an}与{bn}的通项公式;
(2)设数列{cn}对任意自然数n均有![]() 成立,求c1+c2+…+c2016的值.
成立,求c1+c2+…+c2016的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在数列{an}中,a1=1,a2=2,数列{anan+1}是公比为q (q>0)的等比数列,则数列{an}的前2n项和S2n=____________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知抛物线x2=y,点![]() ,抛物线上的点
,抛物线上的点![]() ,过点B作直线AP的垂线,垂足为Q.
,过点B作直线AP的垂线,垂足为Q.
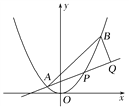
(1)求直线AP斜率的取值范围;
(2)求|PA|·|PQ|的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com