
【题目】过点![]() 的动直线l与y轴交于点
的动直线l与y轴交于点![]() ,过点T且垂直于l的直线
,过点T且垂直于l的直线![]() 与直线
与直线![]() 相交于点M.
相交于点M.
(1)求M的轨迹方程;
(2)设M位于第一象限,以AM为直径的圆![]() 与y轴相交于点N,且
与y轴相交于点N,且![]() ,求
,求![]() 的值.
的值.
 天天练口算系列答案
天天练口算系列答案科目:高中数学 来源: 题型:
【题目】已知数列{an}满足a1=1,an=![]() (n∈N*,n≥2),数列{bn}满足关系式bn=
(n∈N*,n≥2),数列{bn}满足关系式bn=![]() (n∈N*).
(n∈N*).
(1)求证:数列{bn}为等差数列;
(2)求数列{an}的通项公式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,以原点
中,以原点![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系.已知直线
轴正半轴为极轴建立极坐标系.已知直线![]() 的极坐标方程为
的极坐标方程为![]() ,曲线
,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)写出直线![]() 和曲线
和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)过动点![]() 且平行于
且平行于![]() 的直线交曲线
的直线交曲线![]() 于
于![]() 两点,若
两点,若![]() ,求动点
,求动点![]() 到直线
到直线![]() 的最近距离.
的最近距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() ,点
,点![]() ,
,![]() ,
,![]() 分别为椭圆的左焦点、右顶点和下顶点,
分别为椭圆的左焦点、右顶点和下顶点,![]() 的面积为
的面积为![]() ,且椭圆的离心率为
,且椭圆的离心率为![]() .
.
(1)求椭圆的标准方程;
(2)若点![]() 为椭圆
为椭圆![]() 上一点,直线
上一点,直线![]() 与椭圆
与椭圆![]() 交于不同的两点
交于不同的两点![]() ,
,![]() ,且
,且![]() (点
(点![]() 为坐标原点),求
为坐标原点),求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某省即将实行新高考,不再实行文理分科.某校为了研究数学成绩优秀是否对选择物理有影响,对该校2018级的1000名学生进行调查,收集到相关数据如下:
(1)根据以上提供的信息,完成![]() 列联表,并完善等高条形图;
列联表,并完善等高条形图;
选物理 | 不选物理 | 总计 | |
数学成绩优秀 | |||
数学成绩不优秀 | 260 | ||
总计 | 600 | 1000 |
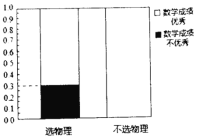
(2)能否在犯错误的概率不超过0.05的前提下认为数学成绩优秀与选物理有关?
附:
临界值表:
| 0.10 | 0.05 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() ,
,![]() ,
,![]() ,给出以下四个命题:①
,给出以下四个命题:①![]() 为偶函数;②
为偶函数;②![]() 为偶函数;③
为偶函数;③![]() 的最小值为0;④
的最小值为0;④![]() 有两个零点.其中真命题的是( ).
有两个零点.其中真命题的是( ).
A.②④B.①③C.①③④D.①④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为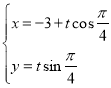 (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)求直线![]() 的普通方程及曲线
的普通方程及曲线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)已知点![]() 是曲线
是曲线![]() 上的任意一点,当点
上的任意一点,当点![]() 到直线
到直线![]() 的距离最大时,求经过点
的距离最大时,求经过点![]() 且与直线
且与直线![]() 平行的直线
平行的直线![]() 的方程.
的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com