
【题目】在![]() 中,
中, ![]() 分别是角
分别是角![]() 的对边,已知
的对边,已知![]() ,现有以下判断:
,现有以下判断:
①![]() 不可能等于15; ②
不可能等于15; ②![]() ;
;
③作![]() 关于
关于![]() 的对称点
的对称点![]() 的最大值是
的最大值是![]() ;
;
④若![]() 为定点,则动点
为定点,则动点![]() 的轨迹围成的封闭图形的面积是
的轨迹围成的封闭图形的面积是![]() 。请将所有正确的判断序号填在横线上______________。
。请将所有正确的判断序号填在横线上______________。
【答案】①②③
【解析】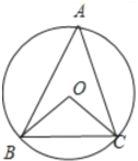
设![]() 的外接圆半径为
的外接圆半径为![]() ,则
,则![]() ,
, ![]() ,
, ![]()
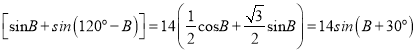 ,
, ![]() ,故①正确;
,故①正确; ![]() ,
, ![]() ,故②正确;
,故②正确; ![]()
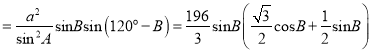
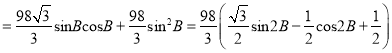
![]() ,
, ![]() 当
当![]() 即
即![]() 时,
时, ![]() 取得最大值
取得最大值![]() ,设
,设![]() 到直线
到直线![]() 的距离为
的距离为![]() ,则
,则![]() ,于是
,于是![]() 的最大值为
的最大值为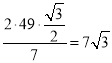 ,故③正确;如图所示,假设线段
,故③正确;如图所示,假设线段![]() 水平放置,
水平放置, ![]() 在直线
在直线![]() 上方,显然
上方,显然![]() 在圆
在圆![]() 的优弧
的优弧![]() 上运动,
上运动, ![]() ,
, ![]() ,
, ![]() ,同理可知当
,同理可知当![]() 直线
直线![]() 下方时,以上结论也成立,
下方时,以上结论也成立, ![]() 点
点![]() 的轨迹围成的封闭图形的面积是
的轨迹围成的封闭图形的面积是![]() ,故④错误,故答案为①②③.
,故④错误,故答案为①②③.
【 方法点睛】本题主要通过对多个命题真假的判断,主要综合正弦定理以及三角函数的恒等变形,属于难题.这种题型综合性较强,也是高考的命题热点,同学们往往因为某一处知识点掌握不好而导致“全盘皆输”,因此做这类题目更要细心、多读题,尽量挖掘出题目中的隐含条件,另外,要注意从简单的自己已经掌握的知识点入手,然后集中精力突破较难的命题.


 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,
为参数, ![]() ),以原点
),以原点![]() 为极点,
为极点, ![]() 轴正半轴为极轴,建立极坐标系,曲线
轴正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 与
与![]() 的直角坐标方程;
的直角坐标方程;
(2)当![]() 与
与![]() 有两个公共点时,求实数
有两个公共点时,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动点![]() 到定点
到定点![]() 的距离比
的距离比![]() 到定直线
到定直线![]() 的距离小1.
的距离小1.
(Ⅰ)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(Ⅱ)过点![]() 任意作互相垂直的两条直线
任意作互相垂直的两条直线![]() ,分别交曲线
,分别交曲线![]() 于点
于点![]() 和
和![]() .设线段
.设线段![]() ,
, ![]() 的中点分别为
的中点分别为![]() ,求证:直线
,求证:直线![]() 恒过一个定点;
恒过一个定点;
(Ⅲ)在(Ⅱ)的条件下,求![]() 面积的最小值.
面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,椭圆
中,椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() 离心率为
离心率为![]() ,两准线之间的距离为8,点
,两准线之间的距离为8,点![]() 在椭圆
在椭圆![]() 上,且位于第一象限,过点
上,且位于第一象限,过点![]() 作直线
作直线![]() 的垂线
的垂线![]() ,过点
,过点![]() 作直线
作直线![]() 的垂线
的垂线![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若直线![]() 的交点
的交点![]() 在椭圆
在椭圆![]() 上,求点
上,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 与直线
与直线![]() 相切.
相切.
(1)若直线![]() 与圆
与圆![]() 交于
交于![]() 两点,求
两点,求![]() ;
;
(2)设圆![]() 与
与![]() 轴的负半轴的交点为
轴的负半轴的交点为![]() ,过点
,过点![]() 作两条斜率分别为
作两条斜率分别为![]() 的直线交圆
的直线交圆![]() 于
于![]() 两点,且
两点,且![]() ,试证明直线
,试证明直线![]() 恒过一定点,并求出该定点的坐标.
恒过一定点,并求出该定点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,圆
中,圆![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),直线
为参数),直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).
为参数).
(1)若直线![]() 与圆
与圆![]() 相交于
相交于![]() ,
, ![]() 两点,求弦长
两点,求弦长![]() ;
;
(2)以该直角坐标系的原点![]() 为极点,
为极点, ![]() 轴的非负半轴为极轴建立极坐标系,圆
轴的非负半轴为极轴建立极坐标系,圆![]() 的极坐标方程为
的极坐标方程为![]() ,圆
,圆![]() 和圆
和圆![]() 的交点为
的交点为![]() ,
, ![]() ,求弦
,求弦![]() 所在直线的直角坐标方程.
所在直线的直角坐标方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 为圆
为圆![]() 的圆心,
的圆心, ![]() 是圆上的动点,点
是圆上的动点,点![]() 在圆的半径
在圆的半径![]() 上,且有点
上,且有点![]() 和
和![]() 上的点
上的点![]() ,满足
,满足![]() ,
, ![]() .
.
(1)当点![]() 在圆上运动时,求点
在圆上运动时,求点![]() 的轨迹方程;
的轨迹方程;
(2)若斜率为![]() 的直线
的直线![]() 与圆
与圆![]() 相切,直线
相切,直线![]() 与(1)中所求点
与(1)中所求点![]() 的轨迹交于不同的两点
的轨迹交于不同的两点![]() ,
, ![]() ,
, ![]() 是坐标原点,且
是坐标原点,且![]() 时,求
时,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,半径为2的圆内有两条圆弧,一质点M自点A开始沿弧A-B-C-O-A-D-C做匀速运动,则其在水平方向(向右为正)的速度![]() 的图像大致为( )
的图像大致为( )


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com