
【题目】已知函数![]() =
=![]() (
(![]() ).
).
(Ⅰ)当![]() =-3时,求
=-3时,求![]() 的极值;
的极值;
(Ⅱ)当![]() >1时,
>1时,![]() >0,求实数
>0,求实数![]() 的取值范围.
的取值范围.
【答案】见解析
【解析】(Ⅰ)当![]() =-3时,
=-3时,![]() =
=![]() ,定义域为(0,﹢∞),
,定义域为(0,﹢∞),
![]() =
=![]() =
=![]() =
=![]() ,
,
当0<![]() <1或
<1或![]() >2时,
>2时,![]() >0,当1<
>0,当1<![]() <2时,
<2时,![]() <0,故
<0,故![]() 在(0,1)上是增函数,在(1,2)是减函数,在(2,+∞)上是增函数,
在(0,1)上是增函数,在(1,2)是减函数,在(2,+∞)上是增函数,
∴当![]() =1时,
=1时,![]() 取极大值1,当
取极大值1,当![]() =2时,
=2时,![]() 取极小值
取极小值![]() =
=![]() .(5分)
.(5分)
(Ⅱ)∵![]() =
=![]() =
=![]() =
=![]() (
(![]() >1),
>1),
当![]() ≥-2时,-(
≥-2时,-(![]() +1)≤1,
+1)≤1,![]() >0,∴
>0,∴![]() 在(1,+∞)上是增函数,
在(1,+∞)上是增函数,
∴当![]() >1时,
>1时,![]() >
>![]() =1+2+
=1+2+![]() +1=
+1=![]() +4≥0,解得
+4≥0,解得![]() ≥
≥![]() ,∴
,∴![]() ≥
≥![]() ;
;
当![]() <-2时,-(
<-2时,-(![]() +1)>1,当1<
+1)>1,当1<![]() <-(
<-(![]() +1)时,
+1)时,![]() <0,当
<0,当![]() >-(
>-(![]() +1)时,
+1)时,![]() >0,∴
>0,∴![]() 在(1,-(
在(1,-(![]() +1))上是减函数,在(-(
+1))上是减函数,在(-(![]() +1),+∞)上是增函数,
+1),+∞)上是增函数,
∴当![]() =-(
=-(![]() +1)时,
+1)时,![]() =
=![]() =
=![]() ,
,
要使![]() >0对
>0对![]() >1恒成立,则
>1恒成立,则![]() =
=![]() >0,
>0,
即![]() ,∴
,∴![]() ,解得
,解得![]() <
<![]() <2,
<2,
综上所述,实数![]() 的取值范围为(
的取值范围为(![]() ,+∞).(12分)
,+∞).(12分)


 ABC考王全优卷系列答案
ABC考王全优卷系列答案科目:高中数学 来源: 题型:
【题目】春节来临,有农民工兄弟![]() 、
、![]() 、
、![]() 、
、![]() 四人各自通过互联网订购回家过年的火车票,若订票成功即可获得火车票,即他们获得火车票与否互不影响.若
四人各自通过互联网订购回家过年的火车票,若订票成功即可获得火车票,即他们获得火车票与否互不影响.若![]() 、
、![]() 、
、![]() 、
、![]() 获得火车票的概率分别是
获得火车票的概率分别是![]() ,其中
,其中![]() ,又
,又![]() 成等比数列,且
成等比数列,且![]() 、
、![]() 两人恰好有一人获得火车票的概率是
两人恰好有一人获得火车票的概率是![]() .
.
(1)求![]() 的值;
的值;
(2)若![]() 、
、![]() 是一家人且两人都获得火车票才一起回家,否则两人都不回家.设
是一家人且两人都获得火车票才一起回家,否则两人都不回家.设![]() 表示
表示![]() 、
、![]() 、
、![]() 、
、![]() 能够回家过年的人数,求
能够回家过年的人数,求![]() 的分布列和期望
的分布列和期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】△ABC的内角A、B、C所对的边分别为a,b,c. (Ⅰ)若a,b,c成等差数列,证明:sinA+sinC=2sin(A+C);
(Ⅱ)若a,b,c成等比数列,且c=2a,求cosB的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市为了考核甲,乙两部门的工作情况,随机访问了50位市民,根据这50位市民对这两部门的评分(评分越高表明市民的评价越高),绘制茎叶图如下:

(1)分别估计该市的市民对甲,乙两部门评分的中位数;
(2)分别估计该市的市民对甲,乙两部门的评分高于90的概率;
(3)根据茎叶图分析该市的市民对甲,乙两部门的评价.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某厂家拟在2017年举行促销活动,经调查测算,该产品的年销售量(即该厂的年产量)![]() (单位:万件)与年促销费用
(单位:万件)与年促销费用![]() (单位:万元)(
(单位:万元)(![]() )满足
)满足![]() (
(![]() 为常数),如果不搞促销活动,则该产品的年销售量只能是1万件.已知2017年生产该产品的固定投入为8万元.每生产1万件该产品需要再投入16万元,厂家将每件产品的销售价格定为每件产品年平均成本的1.5倍(产品成本包括固定投入和再投入两部分资金).
为常数),如果不搞促销活动,则该产品的年销售量只能是1万件.已知2017年生产该产品的固定投入为8万元.每生产1万件该产品需要再投入16万元,厂家将每件产品的销售价格定为每件产品年平均成本的1.5倍(产品成本包括固定投入和再投入两部分资金).
(1)将2017年该产品的利润![]() (单位:万元)表示为年促销费用
(单位:万元)表示为年促销费用![]() (单位:万元)的函数;
(单位:万元)的函数;
(2)该厂家2017年的促销费用投入多少万元时,厂家的利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2016年中国(云南赛区)三对三篮球联赛在昆明市体育局的大力支持下,圆满顺利结束.组织方统计了来自![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 球队的男子的平均身高与本次比赛的平均得分,如下表所示:
球队的男子的平均身高与本次比赛的平均得分,如下表所示:
球队 |
|
|
|
|
|
平均身高 | 170 | 174 | 176 | 181 | 179 |
平均得分 | 62 | 64 | 66 | 70 | 68 |
(2)若![]() 队平均身高为
队平均身高为![]()
![]() ,根据(1)中所求得的回归方程,预测
,根据(1)中所求得的回归方程,预测![]() 队的平均得分.(精确到个位)
队的平均得分.(精确到个位)
注:回归方程![]() 中斜率和截距最小二乘估计公式分别为
中斜率和截距最小二乘估计公式分别为
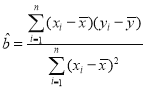 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2016年11月,第十一届中国(珠海)国际航空航天博览会开幕式当天,歼-20的首次亮相给观众留下了极深的印象.某参赛国展示了最新研制的两种型号的无人机,先从参观人员中随机抽取100人对这两种型号的无人机进行评价,评价分为三个等级:优秀、良好、合格.由统计信息可知,甲型号无人机被评为优秀的频率为![]() 、良好的频率为
、良好的频率为![]() ;乙型号无人机被评为优秀的频率为
;乙型号无人机被评为优秀的频率为![]() ,且被评为良好的频率是合格的频率的5倍.
,且被评为良好的频率是合格的频率的5倍.
(1) 求这100人中对乙型号无人机评为优秀和良好的人数;
(2) 如果从这100人中按对甲型号无人机的评价等级用分层抽样的方法抽取5人,然后从其他对乙型号无人机评优秀、良好的人员中各选取1人进行座谈会,会后从这7人中随机抽取2人进行现场操作体验活动,求进行现场操作体验活动的2人都评优秀的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com