
【题目】
对函数Φ(x),定义fk(x)=Φ(x-mk)+nk(其中x∈(mk,m+mk],k∈Z,m>0,n>0,且m、n为常数)为Φ(x)的第k阶阶梯函数,m叫做阶宽,n叫做阶高,已知阶宽为2,阶高为3.
(1)当Φ(x)=2x时 ①求f0(x)和fk(x)的解析式; ②求证:Φ(x)的各阶阶梯函数图象的最高点共线;
(2)若Φ(x)=x2,则是否存在正整数k,使得不等式fk(x)<(1-3k)x+4k2+3k-1有解?若存在,求出k的值;若不存在,请说明理由.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】将函数f(x)=cos(2x![]() )的图象向左平移
)的图象向左平移![]() 个单位长度后,得到函数g(x)的图象,则下列结论中正确的是_____.(填所有正确结论的序号)
个单位长度后,得到函数g(x)的图象,则下列结论中正确的是_____.(填所有正确结论的序号)
①g(x)的最小正周期为4π;
②g(x)在区间[0,![]() ]上单调递减;
]上单调递减;
③g(x)图象的一条对称轴为x![]() ;
;
④g(x)图象的一个对称中心为(![]() ,0).
,0).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,一楼房高![]() 为
为![]() 米,某广告公司在楼顶安装一块宽
米,某广告公司在楼顶安装一块宽![]() 为
为![]() 米的广告牌,
米的广告牌,![]() 为拉杆,广告牌的倾角为
为拉杆,广告牌的倾角为![]() ,安装过程中,一身高为
,安装过程中,一身高为![]() 米的监理人员
米的监理人员![]() 站在楼前观察该广传牌的安装效果:为保证安全,该监理人员不得站在广告牌的正下方:设
站在楼前观察该广传牌的安装效果:为保证安全,该监理人员不得站在广告牌的正下方:设![]() 米,该监理人员观察广告牌的视角
米,该监理人员观察广告牌的视角![]() .
.
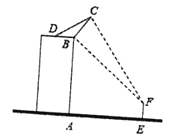
(1)试将![]() 表示为
表示为![]() 的函数;
的函数;
(2)求点![]() 的位置,使
的位置,使![]() 取得最大值.
取得最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设直线l的方程为(a﹣1)x+y+a+3=0,(a∈R).
(1)若直线l在两坐标轴上截距的绝对值相等,求直线l的方程;
(2)若直线l不经过第一象限,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy内,点(![]() )在椭圆E:
)在椭圆E:![]() (a>0,b>0),椭圆E的离心率为
(a>0,b>0),椭圆E的离心率为![]() ,直线l过左焦点F且与椭圆E交于A、B两点
,直线l过左焦点F且与椭圆E交于A、B两点
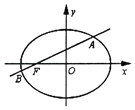
(1)求椭圆E的标准方程;
(2)若动直线l与x轴不重合,在x轴上是否存在定点P,使得PF始终平分∠APB?若存在,请求出点P的坐标:若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的长轴长为
的长轴长为![]() ,焦距为2,抛物线
,焦距为2,抛物线![]() 的准线经过
的准线经过![]() 的左焦点
的左焦点![]() .
.
(1)求![]() 与
与![]() 的方程;
的方程;
(2)直线![]() 经过
经过![]() 的上顶点且
的上顶点且![]() 与
与![]() 交于
交于![]() ,
,![]() 两点,直线
两点,直线![]() ,
,![]() 与
与![]() 分别交于点
分别交于点![]() (异于点
(异于点![]() ),
),![]() (异于点
(异于点![]() ),证明:直线
),证明:直线![]() 的斜率为定值.
的斜率为定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com