
|
|
|
|
| y-1 |
| 2-1 |
| x-3 |
| 1-3 |
|
| 5 |
| 2 |


 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案科目:高中数学 来源: 题型:
| AB |
| AE |
| AC |
| AF |
| 1 |
| λ |
| 4 |
| μ |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 5 |
| c |
| a |
| a |
| c |
| Xn |
查看答案和解析>>
科目:高中数学 来源:学习周报 数学 北师大课标高二版(选修2-2) 2009-2010学年 第27期 总第183期 北师大课标 题型:044
已知Rt△ABC的三条边分别为3,4,5,若该三角形绕着三条边分别旋转一周,所得几何体的体积分别为12π,16π,![]() π,注意到(
π,注意到(![]() )2+(
)2+(![]() )2=(
)2=(![]() )2.将此结果拓展到边长分别为a,b,c(c为斜边长)的一般直角三角形,你能得到什么结论,并证明你的结论.
)2.将此结果拓展到边长分别为a,b,c(c为斜边长)的一般直角三角形,你能得到什么结论,并证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知Rt△ABC的两直角边AC=2,BC=3,P为斜边上一
点,沿CP将此直角三角形折成直二面角A—CP—B,当AB=71/2时,求二面角P—AC—B的大小。


查看答案和解析>>
科目:高中数学 来源: 题型:解答题
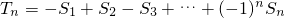 ,求满足不等式
,求满足不等式 的所有n的值;
的所有n的值;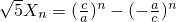 (n∈N+),证明:数列{
(n∈N+),证明:数列{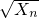 }中的任意连续三项为边长均可以构成直角三角形,且Xn是正整数.
}中的任意连续三项为边长均可以构成直角三角形,且Xn是正整数.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com