已知曲线x2+y2-4x-2y-k=0表示的图象为圆.
(1)若k=15,求过该曲线与直线x-2y+5=0的交点,且面积最小的圆的方程.
(2)若该圆关于直线x+y-4=0的对称圆与直线6x+8y-59=0相切,求实数k的值.
【答案】
分析:(1)先设圆心A坐标并把k代入已知方程配方后求A的坐标,由A在x-2y+5=0上时此圆的面积最小,两个圆心的连线与直线垂直,利用斜率之积等于-1和A在直线上列出方程组求圆心的坐标,再利用弦心距、半径和弦的一半关系求出半径;
(2)根据两个圆心关于直线对称关系,求出对称圆心的坐标,再由对称圆与6x+8y-59=0相切,即圆心到直线的距离等于半径求出圆的半径r,即
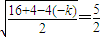
再求出k.
解答:解:(1)设所求圆的圆心坐标为A(x
,y
)
当k=15时,代入x
2+y
2-4x-2y-k=0,化简得(x-2)
2+(y-1)
2=20,
∴圆心B(2,1),到直线x-2y+5=0的距离为
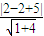
=
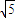
,
当相交弦为所求圆的直径时,圆的面积最小,即圆心A在直线x-2y+5=0上;
则
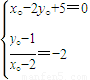
,解得
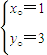
,
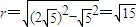
∴所求圆的方程为:(x-1)
2+(y-3)
2=15
(2)设圆心B(2,1)关于y=-x+4的对称圆的圆心为C(x,y),
∴
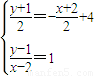
,解得x=3,y=2;则 C(3,2)
∵对称圆C与直线6x+8y-59=0相切,
∴点(3,2)到6x+8y-59=0的距离为
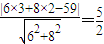
即
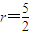
由x
2+y
2-4x-2y-k=0得
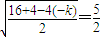
解得,
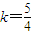 点评:
点评:本题考查了圆与直线的综合问题,利用弦心距、半径和弦的一半构成直角三角形,两个圆关于直线对称时有半径相等和圆心对称关系及相切的条件求出半径,再求出k的值.

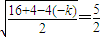 再求出k.
再求出k.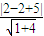 =
=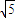 ,
,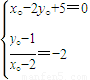 ,解得
,解得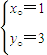 ,
,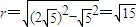
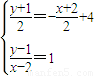 ,解得x=3,y=2;则 C(3,2)
,解得x=3,y=2;则 C(3,2)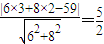
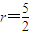
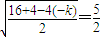
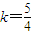


 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案