
【题目】如图,已知椭圆![]() ,椭圆的长轴长为8,离心率为
,椭圆的长轴长为8,离心率为![]() .
.

![]() 求椭圆方程;
求椭圆方程;
![]() 椭圆内接四边形ABCD的对角线交于原点,且
椭圆内接四边形ABCD的对角线交于原点,且![]() ,求四边形ABCD周长的最大值与最小值.
,求四边形ABCD周长的最大值与最小值.
【答案】(1)![]() ; (2)四边形ABCD的周长的最小值为
; (2)四边形ABCD的周长的最小值为![]() ,最大值为20..
,最大值为20..
【解析】
(1)由题意可得a=4,运用离心率公式可得c,再由a,b,c的关系可得b,进而得到椭圆方程;
(2)由题意的对称性可得四边形ABCD为平行四边形,运用向量的数量积的性质,可得![]() 2
2![]() 2,即有四边形ABCD为菱形,即有AC⊥BD,讨论直线AC的斜率为0,可得最大值;不为0,设出直线AC的方程为y=kx,(k>0),则BD的方程为y
2,即有四边形ABCD为菱形,即有AC⊥BD,讨论直线AC的斜率为0,可得最大值;不为0,设出直线AC的方程为y=kx,(k>0),则BD的方程为y![]() x,代入椭圆方程,求得A,D的坐标,运用两点的距离公式,化简整理,由二次函数的最值求法,可得最小值.
x,代入椭圆方程,求得A,D的坐标,运用两点的距离公式,化简整理,由二次函数的最值求法,可得最小值.
![]() 由题意可得
由题意可得![]() ,即
,即![]() ,
,
由![]() ,可得
,可得![]() ,
,![]() ,
,
即有椭圆的方程为![]() ;
;
![]() 由题意的对称性可得四边形ABCD为平行四边形,
由题意的对称性可得四边形ABCD为平行四边形,
由![]() ,可得
,可得![]() ,
,
即![]() ,
,
可得![]() ,即有四边形ABCD为菱形,
,即有四边形ABCD为菱形,
即有![]() ,
,
设直线AC的方程为![]() ,
,![]() ,则BD的方程为
,则BD的方程为![]() ,
,
代入椭圆方程可得![]() ,
,
可设![]() ,
,
同理可得![]() ,
,
即有![]()
![]() ,
,
令![]() ,
,
即有 ,
,
由![]() ,
,
即有![]() ,即
,即![]() 时,
时,![]() 取得最小值,且为
取得最小值,且为![]() ;
;
又当AC的斜率为0时,BD为短轴,即有ABCD的周长取得最大值,且为20.
综上可得四边形ABCD的周长的最小值为![]() ,最大值为20.
,最大值为20.


 新思维寒假作业系列答案
新思维寒假作业系列答案科目:高中数学 来源: 题型:
【题目】下列命题正确的是( )
A.复数z1,z2的模相等,则z1,z2是共轭复数
B.z1,z2都是复数,若z1+z2是虚数,则z1不是z2的共轭复数
C.复数z是实数的充要条件是z=![]() (
(![]() 是z的共轭复数)
是z的共轭复数)
D.已知复数z1=-1+2i,z2=1-i,z3=3-2i(i是虚数单位),它们对应的点分别为A,B,C,O为坐标原点,若![]() (x,y∈R),则x+y=1
(x,y∈R),则x+y=1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知中心在原点,焦点在x轴上的椭圆C的离心率为![]() ,且经过点M(1,
,且经过点M(1,![]() ),过点P(2,1)的直线l与椭圆C相交于不同的两点A,B.
),过点P(2,1)的直线l与椭圆C相交于不同的两点A,B.
(1)求椭圆C的方程;
(2)是否存在直线l,满足![]() ?若存在,求出直线l的方程;若不存在,请说明理由.
?若存在,求出直线l的方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高级中学今年高一年级招收“国际班”学生![]() 人,学校为这些学生开辟了直升海外一流大学的绿色通道,为了逐步提高这些学生与国际教育接轨的能力,将这
人,学校为这些学生开辟了直升海外一流大学的绿色通道,为了逐步提高这些学生与国际教育接轨的能力,将这![]() 人分为三个批次参加国际教育研修培训,在这三个批次的学生中男、女学生人数如下表:
人分为三个批次参加国际教育研修培训,在这三个批次的学生中男、女学生人数如下表:
第一批次 | 第二批次 | 第三批次 | |
女 |
|
|
|
男 |
|
|
|
已知在这![]() 名学生中随机抽取
名学生中随机抽取![]() 名,抽到第一批次、第二批次中女学生的概率分别是
名,抽到第一批次、第二批次中女学生的概率分别是![]() .
.
(1)求![]() 的值;
的值;
(2)为了检验研修的效果,现从三个批次中按分层抽样的方法抽取![]() 名同学问卷调查,则三个批次被选取的人数分别是多少?
名同学问卷调查,则三个批次被选取的人数分别是多少?
(3)若从第(2)小问选取的学生中随机选出两名学生进行访谈,求“参加访谈的两名同学至少有一个人来自第一批次”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 和
和![]() 满足
满足![]() ,
,![]() ,
,![]() ,
,![]() .
.
(1)证明:![]() 是等比数列,
是等比数列,![]() 是等差数列;
是等差数列;
(2)求![]() 和
和![]() 的通项公式;
的通项公式;
(3)令 ,求数列
,求数列![]() 的前
的前![]() 项和
项和![]() 的通项公式,并求数列
的通项公式,并求数列![]() 的最大值、最小值,并指出分别是第几项.
的最大值、最小值,并指出分别是第几项.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 和动点
和动点![]() ,以线段
,以线段![]() 为直径的圆内切于圆
为直径的圆内切于圆![]() .
.
(1)求动点![]() 的轨迹方程;
的轨迹方程;
(2)已知点![]() ,
, ![]() ,经过点
,经过点![]() 的直线
的直线![]() 与动点
与动点![]() 的轨迹交于
的轨迹交于![]() ,
, ![]() 两点,求证:直线
两点,求证:直线![]() 与直线
与直线![]() 的斜率之和为定值.
的斜率之和为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4—4:极坐标与参数方程
在平面直角坐标系![]() 中,将曲线
中,将曲线![]() (
(![]() 为参数) 上任意一点
为参数) 上任意一点![]() 经过伸缩变换
经过伸缩变换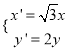 后得到曲线
后得到曲线![]() 的图形.以坐标原点
的图形.以坐标原点![]() 为极点,x轴的非负半轴为极轴,取相同的单位长度建立极坐标系,已知直线
为极点,x轴的非负半轴为极轴,取相同的单位长度建立极坐标系,已知直线![]() .
.
(Ⅰ)求曲线![]() 和直线
和直线![]() 的普通方程;
的普通方程;
(Ⅱ)点P为曲线![]() 上的任意一点,求点P到直线
上的任意一点,求点P到直线![]() 的距离的最大值及取得最大值时点P的坐标.
的距离的最大值及取得最大值时点P的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学为了解高一学生的视力健康状况,在高一年级体检活动中采用统一的标准对数视力表,按照《中国学生体质健康监测工作手册》的方法对1039名学生进行了视力检测,判断标准为:双眼裸眼视力![]() 为视力正常,
为视力正常, ![]() 为视力低下,其中
为视力低下,其中![]() 为轻度,
为轻度, ![]() 为中度,
为中度, ![]() 为重度.统计检测结果后得到如图所示的柱状图.
为重度.统计检测结果后得到如图所示的柱状图.
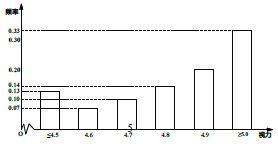
(1)求该校高一年级轻度近视患病率;
(2)根据保护视力的需要,需通知检查结果为“重度近视”学生的家长带孩子去医院眼科进一步检查和确诊,并开展相应的矫治,则该校高一年级需通知的家长人数约为多少人?
(3)若某班级6名学生中有2人为视力正常,则从这6名学生中任选2人,恰有1人视力正常的概率是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com