
【题目】(题文)如图,在多面体![]() 中,
中, ![]() 是正方形,
是正方形, ![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
, ![]() ,点
,点![]() 为棱
为棱![]() 的中点.
的中点.
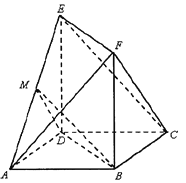
(1)求证:平面![]() 平面
平面![]() ;
;
(2)若![]() ,求三棱锥
,求三棱锥![]() 的体积.
的体积.
科目:高中数学 来源: 题型:
【题目】已知定义在R上的函数f(x)=x2+|x﹣m|(m为实数)是偶函数,记a=f( ![]() e),b=f(log3π),c=f(em)(e为自然对数的底数),则a,b,c的大小关系( )
e),b=f(log3π),c=f(em)(e为自然对数的底数),则a,b,c的大小关系( )
A.a<b<c
B.a<c<b
C.c<a<b
D.c<b<a
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着国民生活水平的提高,利用长假旅游的人越来越多,其公司统计了2012到2016年五年间本公司职工每年春节期间外出旅游的家庭数,具体统计数据如表所示:
年份x | 2012 | 2013 | 2014 | 2015 | 2016 |
家庭数y | 6 | 10 | 16 | 22 | 26 |
(1)利用所给数据,求出春节期间外出旅游的家庭数与年份之间的回归直线方程y=bx+a,判断它们之间是否是正相关还是负相关;
(2)根据所求的直线方程估计该公司2019年春节期间外出的旅游的家庭数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】公差不为零的等差数列{an}中,a1 , a2 , a5成等比数列,且该数列的前10项和为100,数列{bn}的前n项和为Sn , 且满足Sn= ![]() ,n∈N* .
,n∈N* .
(1)求数列{an},{bn}的通项公式;
(2)记得数列{ ![]() }的前n项和为Tn , 求Tn的取值范围.
}的前n项和为Tn , 求Tn的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知美国苹果公司生产某款iPhone手机的年固定成本为40万美元,每生产1万只还需另投入16万美元.设苹果公司一年内共生产该款iPhone手机x万只并全部销售完,每万只的销售收入为R(x)万美元,且R(x)=
(1)写出年利润W(万美元)关于年产量x(万只)的函数解析式;
(2)当年产量为多少万只时,苹果公司在该款iPhone手机的生产中所获得的利润最大?并求出最大利润.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
, ![]()
(1)当![]() 时,求函数
时,求函数![]() 的单调区间;
的单调区间;
(2)若函数![]() 在区间
在区间![]() 上有1个零点,求实数
上有1个零点,求实数![]() 的取值范围;
的取值范围;
(3)是否存在正整数![]() ,使得
,使得![]() 在
在![]() 上恒成立?若存在,求出k的最大值;若不存在,说明理由.
上恒成立?若存在,求出k的最大值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知点
中,已知点![]() 和直线
和直线![]() :
:![]() ,设圆
,设圆![]() 的半径为1,圆心在直线
的半径为1,圆心在直线![]() 上.
上.
(Ⅰ)若圆心![]() 也在直线
也在直线![]() 上,过点
上,过点![]() 作圆
作圆![]() 的切线.
的切线.
(1)求圆![]() 的方程;(2)求切线的方程;
的方程;(2)求切线的方程;
(Ⅱ)若圆![]() 上存在点
上存在点![]() ,使
,使![]() ,求圆心
,求圆心![]() 的横坐标
的横坐标![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com