设
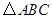
的内角
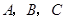
所对的边长分别为
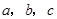
,且
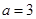
,A=
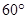
,
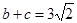
.
(1)求函数
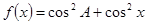
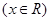
的单调递增区间及最大值;
(2)求
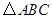
的面积的大小
试题分析:(1)将
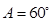
代入函数
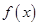
,并将
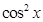
用二倍角公式降幂,将函数
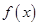
化简变形为
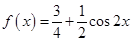
,将角
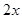
视为整体代入余弦的单调增区间内,可解得
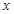
,即可得函数
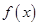
的单调区间。当
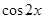
取得最大值1时,函数
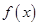
同时取得最大值。(2)根据已知条件由余弦定理可得
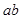
,根据三角形面积公式
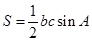
可求其面积。
试题解析:(1)

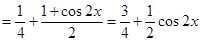
,由
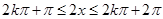
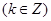
,可得函数
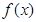
的单调递增区间为
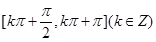
,当且仅当
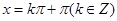
时
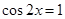
,函数
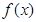
取得最大值,其最大值是
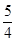
.
(2).由余弦定理
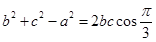
得
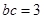
,由此可得
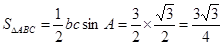
.
练习册系列答案
相关习题
科目:高中数学
来源:不详
题型:解答题
已知函数
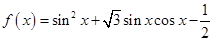
,
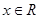
.
(1)求函数
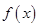
的最小正周期;
(2)在
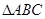
中,角
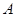
、
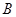
、
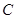
的对边分别为
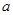
、
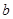
、
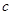
,且满足
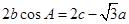
,求
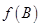
的值.
查看答案和解析>>
科目:高中数学
来源:不详
题型:填空题
已知函数
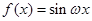
,
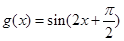
,有下列命题:
①当
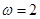
时,函数
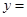
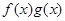
是最小正周期为
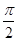
的偶函数;
②当
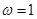
时,
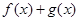
的最大值为
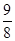
;
③当
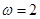
时,将函数
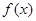
的图象向左平移
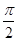
可以得到函数
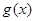
的图象.
其中正确命题的序号是
(把你认为正确的命题的序号都填上).
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
函数
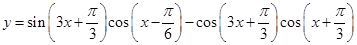
的图象的一条对称轴的方程是( )
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
已知函数

,其导函数

的部分图象如图所示,则函数
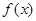
的解析式为( )

查看答案和解析>>
科目:高中数学
来源:不详
题型:填空题
函数
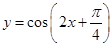
的单调递减区间是____________.
查看答案和解析>>

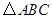 的内角
的内角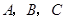 所对的边长分别为
所对的边长分别为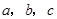 ,且
,且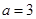 ,A=
,A=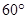 ,
,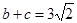 .
.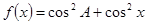
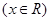 的单调递增区间及最大值;
的单调递增区间及最大值;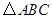 的面积的大小
的面积的大小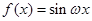 ,
,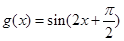 ,有下列命题:
,有下列命题: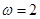 时,函数
时,函数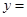
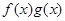 是最小正周期为
是最小正周期为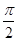 的偶函数;
的偶函数;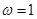 时,
时,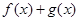 的最大值为
的最大值为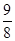 ;
;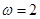 时,将函数
时,将函数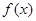 的图象向左平移
的图象向左平移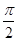 可以得到函数
可以得到函数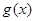 的图象.
的图象.