
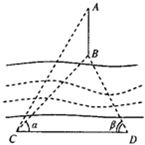
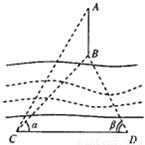
 如图所示,为了测量河对岸地面上A,B两点间的距离,某人在河岸边上选取了C,D两点,使得CD⊥AB,且CD=500(米)现测得∠BCD=α,∠BDC=β,∠ACD=60°,其中cosα=
如图所示,为了测量河对岸地面上A,B两点间的距离,某人在河岸边上选取了C,D两点,使得CD⊥AB,且CD=500(米)现测得∠BCD=α,∠BDC=β,∠ACD=60°,其中cosα=| 3 |
| 5 |
| 3 |
| 3 |
| 5 |
| 4 |
| 5 |
| 2 | ||
|
| 1 | ||
|
| 4 |
| 5 |
| 1 | ||
|
| 3 |
| 5 |
| 2 | ||
|
2
| ||
| 5 |
| BC |
| sinD |
| CD |
| sin∠CBD |
| CD |
| sin∠CBD |
| 2 | ||
|
| 500 | ||||
|
| ||
| 2 |
| 3 |
| 5 |
| 1 |
| 2 |
| 4 |
| 5 |
3
| ||
| 10 |
| AB |
| sin∠ACB |
| BC |
| sinA |
| BC |
| sinA |
3
| ||
| 10 |
| 500 | ||
|
| 3 |


 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案科目:高中数学 来源: 题型:
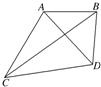 如图所示,为了测量河对岸A,B两点间的距离,在这一岸定一基线CD,现已测出CD=a和∠ACD=60°,∠BCD=30°,∠BDC=105°,∠ADC=60°,试求AB的长.
如图所示,为了测量河对岸A,B两点间的距离,在这一岸定一基线CD,现已测出CD=a和∠ACD=60°,∠BCD=30°,∠BDC=105°,∠ADC=60°,试求AB的长.查看答案和解析>>
科目:高中数学 来源:2010-2011学年福建省高三第二次月考理科数学卷 题型:解答题
(本题满分13分)
如图所示,为了测量河对岸A,B两点间的距离,在这一岸定一基线CD,现已测出
CD=a和∠ACD=60°,∠BCD=30°,∠BDC=105°,∠ADC=60°,试求AB的长.

查看答案和解析>>
科目:高中数学 来源: 题型:解答题
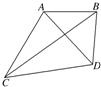 如图所示,为了测量河对岸A,B两点间的距离,在这一岸定一基线CD,现已测出CD=a和∠ACD=60°,∠BCD=30°,∠BDC=105°,∠ADC=60°,试求AB的长.
如图所示,为了测量河对岸A,B两点间的距离,在这一岸定一基线CD,现已测出CD=a和∠ACD=60°,∠BCD=30°,∠BDC=105°,∠ADC=60°,试求AB的长.查看答案和解析>>
科目:高中数学 来源:2009-2010学年江苏省苏州市高一(下)期末数学试卷(解析版) 题型:解答题
 ,tanβ=2.求:
,tanβ=2.求: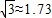 )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com