
【题目】已知![]() ,直线
,直线![]() 与函数
与函数![]() 的图象在
的图象在![]() 处相切,设
处相切,设![]() ,若在区间[1,2]上,不等式
,若在区间[1,2]上,不等式![]() 恒成立.则实数m( )
恒成立.则实数m( )
A. 有最大值![]() B. 有最大值e C. 有最小值e D. 有最小值
B. 有最大值e C. 有最小值e D. 有最小值![]()
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() (
(![]() )和圆
)和圆![]() :
:![]() ,
,![]() 分别是椭圆的左、右两焦点,过
分别是椭圆的左、右两焦点,过![]() 且倾斜角为
且倾斜角为![]() (
(![]() )的动直线
)的动直线![]() 交椭圆
交椭圆![]() 于
于![]() 两点,交圆
两点,交圆![]() 于
于![]() 两点(如图所示,点
两点(如图所示,点![]() 在
在![]() 轴上方).当
轴上方).当![]() 时,弦
时,弦![]() 的长为
的长为![]() .
.

(1)求圆![]() 与椭圆
与椭圆![]() 的方程;
的方程;
(2)若![]() 依次成等差数列,求直线
依次成等差数列,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,将边长为2的正方形ABCD沿PD、PC翻折至A、B两点重合,其中P是AB中点,在折成的三棱锥A(B)-PDC中,点Q在平面PDC内运动,且直线AQ与棱AP所成角为60,则点Q运动的轨迹是
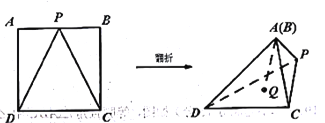
A. 圆 B. 椭圆 C. 双曲线 D. 抛物线
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂的![]() ,
,![]() ,
,![]() 三个不同车间生产同一产品的数量(单位:件)如下表所示.质检人员用分层抽样的方法从这些产品中共抽取6件样品进行检测:
三个不同车间生产同一产品的数量(单位:件)如下表所示.质检人员用分层抽样的方法从这些产品中共抽取6件样品进行检测:
车间 |
|
|
|
数量 | 50 | 150 | 100 |
(1)求这6件样品中来自![]() ,
,![]() ,
,![]() 各车间产品的数量;
各车间产品的数量;
(2)若在这6件样品中随机抽取2件进行进一步检测,求这2件产品来自相同车间的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】时下,租车已经成为新一代的流行词,租车自驾游也慢慢流行起来,某小车租车点的收费标准是,不超过2天按照300元计算;超过两天的部分每天收费标准为100元(不足1天的部分按1天计算).有甲乙两人相互独立来该租车点租车自驾游(各租一车一次),设甲、乙不超过2天还车的概率分别为![]() ;2天以上且不超过3天还车的概率分别
;2天以上且不超过3天还车的概率分别![]() ;两人租车时间都不会超过4天.
;两人租车时间都不会超过4天.
(1)求甲所付租车费用大于乙所付租车费用的概率;
(2)设甲、乙两人所付的租车费用之和为随机变量![]() ,求
,求![]() 的分布列与数学期望
的分布列与数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】新高考改革后,假设某命题省份只统一考试数学和语文,英语学科改为参加等级考试,每年考两次,分别放在每个学年的上下学期,其余六科政治,历史,地理,物理,化学,生物则以该省的省会考成绩为准.考生从中选择三科成绩,参加大学相关院校的录取.
(1)若英语等级考试有一次为优,即可达到某“双一流”院校的录取要求.假设某考生参加每次英语等级考试事件是相互独立的,且该生英语等级考试成绩为优的概率为![]() ,求该考生直到高二下期英语等级考试才为优的概率;
,求该考生直到高二下期英语等级考试才为优的概率;
(2)据预测,要想报考某“双一流”院校,省会考的六科成绩都在95分以上,才有可能被该校录取.假设某考生在省会考六科的成绩,考到95分以上的概率都是![]() ,设该考生在省会考时考到95以上的科目数为
,设该考生在省会考时考到95以上的科目数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() 的定义域为
的定义域为![]() ,对于区间
,对于区间![]() ,若
,若![]() 满足
满足![]() ,则称区间
,则称区间![]() 为函数
为函数![]() 的
的![]() 区间.
区间.
(1)证明:区间![]() 是函数
是函数![]() 的
的![]() 区间;
区间;
(2)若区间![]() 是函数
是函数![]() 的
的![]() 区间,求实数
区间,求实数![]() 的取值范围;
的取值范围;
(3)已知函数![]() 在区间
在区间![]() 上的图象连续不断,且在
上的图象连续不断,且在![]() 上仅有
上仅有![]() 个零点,证明:区间
个零点,证明:区间![]() 不是函数
不是函数![]() 的
的![]() 区间.
区间.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com