
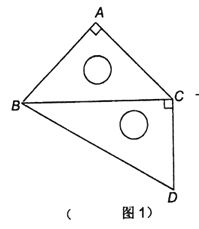
【题目】一副直角三角板(如图1)拼接,将![]() 折起,得到三棱锥
折起,得到三棱锥![]() (如图2).
(如图2).
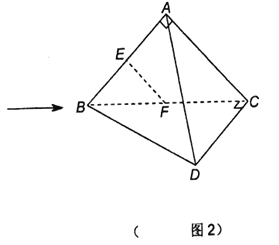
(1)若![]() 分别为
分别为![]() 的中点,求证:
的中点,求证: ![]() 平面
平面![]() ;
;
(2)若平面![]() 平面
平面![]() ,求证:平面
,求证:平面![]() 平面
平面![]() .
.
【答案】(1)证明见解析;(2)证明见解析.
【解析】试题分析:(1)利用三角形中位线的性质,可得![]() ,由线面平行的判定定理可证明
,由线面平行的判定定理可证明![]() 平面
平面![]() ;(2)若平面
;(2)若平面![]() 平面
平面![]() ,可得
,可得![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,由面面垂直的判定定理可证明
,由面面垂直的判定定理可证明
平面![]() 平面
平面![]() .
.
试题解析:(1)因为![]() 分别为
分别为![]() 的中点,所以
的中点,所以![]() ,
,
又![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() .
.
(2)因为平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,
![]() 平面
平面![]() , img src="http://thumb.zyjl.cn/questionBank/Upload/2017/12/29/16/7d737b5e/SYS201712291627592128443134_DA/SYS201712291627592128443134_DA.027.png" width="67" height="19" style="-aw-left-pos:0pt; -aw-rel-hpos:column; -aw-rel-vpos:paragraph; -aw-top-pos:0pt; -aw-wrap-type:inline" />,所以
, img src="http://thumb.zyjl.cn/questionBank/Upload/2017/12/29/16/7d737b5e/SYS201712291627592128443134_DA/SYS201712291627592128443134_DA.027.png" width="67" height="19" style="-aw-left-pos:0pt; -aw-rel-hpos:column; -aw-rel-vpos:paragraph; -aw-top-pos:0pt; -aw-wrap-type:inline" />,所以![]() 平面
平面![]() ,
,
因为![]() 平面
平面![]() ,所以
,所以![]() .
.
又因为![]() ,
, ![]() 平面
平面![]() ,
, ![]() 平面
平面![]() .
.
所以![]() 平面
平面![]() .
.
又![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() .
.
【方法点晴】本题主要考查线面平行的判定定理、线面垂直的判定定理以及面面垂直的判定定理,属于难题.证明线面平行的常用方法:①利用线面平行的判定定理,使用这个定理的关键是设法在平面内找到一条与已知直线平行的直线,可利用几何体的特征,合理利用中位线定理、线面平行的性质或者构造平行四边形、寻找比例式证明两直线平行.②利用面面平行的性质,即两平面平行,在其中一平面内的直线平行于另一平面. 本题(1)是就是利用方法①证明的.


科目:高中数学 来源: 题型:
【题目】如图,已知离心率为![]() 的椭圆
的椭圆![]() :
:![]() 经过点
经过点![]() ,且
,且![]() 是顶点均不与椭圆四个顶点重合的椭圆
是顶点均不与椭圆四个顶点重合的椭圆![]() 一个内接四边形.
一个内接四边形.

(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)若![]() ,试判断
,试判断![]() 的面积是否为定值?若为定值,求出该定值;若不为定值,请说明理由.
的面积是否为定值?若为定值,求出该定值;若不为定值,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】要得到函数y=3cos(2x﹣ ![]() )的图象,可以将函数y=3sin2x的图象( )
)的图象,可以将函数y=3sin2x的图象( )
A.沿x轴向左平移 ![]() 单位
单位
B.沿x轴向右平移 ![]() 单位
单位
C.沿x轴向左平移 ![]() 单位
单位
D.沿x轴向右平移 ![]() 单位
单位
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,已知a、b、c分别是三内角A、B、C所对应的边长,且b2+c2﹣a2=bc
(1)求角A的大小;
(2)若sin2A+sin2B=sin2C,试判断△ABC的形状并求角B的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为响应国家扩大内需的政策,某厂家拟在2016年举行某一产品的促销获得,经调查测算,该产品的年销量(即该厂的年产量)![]() 万件与年促销费用
万件与年促销费用![]() 万元满足
万元满足![]() (
(![]() 为常数).如果不搞促销活动,则该产品的年销量只能是1万件.已知2016年生产该产品的固定投入为6万元,每生产1万件该产品需要再投入12万元,厂家将每件产品的销售价格定为每件产品平均成本的1.5倍(成产投入成本包括生产固定投入和生产再投入两部分).
为常数).如果不搞促销活动,则该产品的年销量只能是1万件.已知2016年生产该产品的固定投入为6万元,每生产1万件该产品需要再投入12万元,厂家将每件产品的销售价格定为每件产品平均成本的1.5倍(成产投入成本包括生产固定投入和生产再投入两部分).
(1)求常数![]() ,并将该厂家2016年该产品的利润
,并将该厂家2016年该产品的利润![]() 万元表示为年促销费用
万元表示为年促销费用![]() 万元的函数;
万元的函数;
(2)该厂家2016年的年促销费用投入多少万元时,厂家利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,将一块直角三角形木板![]() 置于平面直角坐标系中,已知
置于平面直角坐标系中,已知![]() ,点
,点![]() 是三角形木板内一点,现因三角形木板中阴影部分受到损坏,要把损坏部分锯掉,可用经过点
是三角形木板内一点,现因三角形木板中阴影部分受到损坏,要把损坏部分锯掉,可用经过点![]() 的任一直线
的任一直线![]() 将三角形木板锯成
将三角形木板锯成![]() .设直线
.设直线![]() 的斜率为
的斜率为![]() .
.
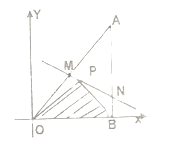
(Ⅰ)求点![]() 的坐标及直线
的坐标及直线![]() 的斜率
的斜率![]() 的范围;
的范围;
(Ⅱ)令![]() 的面积为
的面积为![]() ,试求出
,试求出![]() 的取值范围;
的取值范围;
(Ⅲ)令(Ⅱ)中![]() 的取值范围为集合
的取值范围为集合![]() ,若
,若![]() 对
对![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]()
![]() ,
, ![]() 是坐标原点,
是坐标原点, ![]() 分别为其左右焦点,
分别为其左右焦点, ![]() ,
, ![]() 是椭圆上一点,
是椭圆上一点, ![]() 的最大值为
的最大值为![]()
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)若直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,且
两点,且![]()
(i)求证: ![]() 为定值;
为定值;
(ii)求![]() 面积的取值范围.
面积的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com