练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】某工厂在两个车间，内选取了12个产品，它们的某项指标分布数据的茎叶图如图所示，该项指标不超过19的为合格产品.

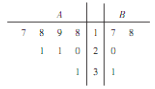
    （1）从选取的产品中在两个车间分别随机抽取2个产品，求两车间都至少抽到一个合格产品的概率；

    （2）若从车间，选取的产品中随机抽取2个产品，用表示车间内产品的个数，求的分布列与数学期望.

    【答案】（1）（2）见解析

    【解析】

    （1）利用茎叶图，求出两个车间的产品数，然后求解概率．（2）写出X的所有可能取值并求出取每个值时对应的概率，得到分布列，然后求解期望即可．

    （1）由茎叶图知，车间内合格的产品数为4，车间内合格的产品数为2，

    则所求概率.

    （2）由题意知，的所有可能取值为0，1，2.

    则，，，

    所以的分布列为

    0

    1

    2

    所以.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    （1）求函数的极值.

    （2）是否存在实数，使得函数在上的最小值为0？若存在，试求出的值：若不存在，请说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图甲，在平面四边形ABCD中，已知∠A＝45°，∠C＝90°，∠ADC＝105°，AB＝BD，现将四边形ABCD沿BD折起，使平面ABD⊥平面BDC(如图乙)，设点E、F分别为棱AC、AD的中点．

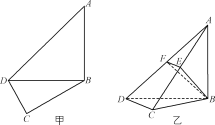
    (1)求证：DC⊥平面ABC；

    (2)求BF与平面ABC所成角的正弦值；

    (3)求二面角B－EF－A的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某公司为了了解本公司职员的早餐费用情况，抽样调査了100位职员的早餐日平均费用（单位：元），得到如图所示的频率分布直方图，图中标注的数字模糊不清.

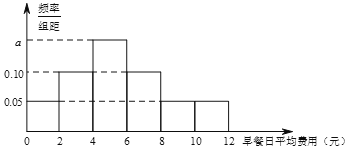
    （1）试根据频率分布直方图求的值，并估计该公司职员早餐日平均费用的众数；

    （2） 已知该公司有1000名职员，试估计该公司有多少职员早餐日平均费用多于8元？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】下列命题正确的是（ ）

    A.已知幂函数在上单调递减则或

    B.函数的有两个零点，一个大于0，一个小于0的一个充分不必要条件是．

    C.已知函数，若，则的取值范围为

    D.已知函数满足，，且与的图像的交点为则的值为8

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某公司为了确定下一年度投入某种产品的宣传费用，需了解年宣传费（单位：万元）对年销量（单位：吨）和年利润（单位：万元）的影响对近6年宣传费和年销量的数据做了初步统计，得到如下数据：

    年份

    2013

    2014

    2015

    2016

    2017

    2018

    年宣传费（万元）

    38

    48

    58

    68

    78

    88

    年销售量（吨）

    16.8

    18.8

    20.7

    22.4

    24.0

    25.5

    经电脑模拟，发现年宣传费（万元）与年销售量（吨）之间近似满足关系式，两边取对数，即，令，即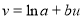对上述数据作了初步处理，得到相关的值如下表：

    75.3

    24.6

    18.3

    101.4

    （1）从表中所给出的6年年销售量数据中任选2年做年销售量的调研，求所选数据中至多有一年年销售量低于21吨的概率．

    （2）根据所给数据，求关于的回归方程；

    （3）若生产该产品的固定成本为200（万元），且每生产1（吨）产品的生产成本为20（万元）（总成本=固定成本+生产成本+年宣传费），销售收入为（万元），假定该产品产销平衡（即生产的产品都能卖掉），2019年该公司计划投入108万元宣传费，你认为该决策合理吗？请说明理由．（其中为自然对数的底数，）

    附：对于一组数据，其回归直线中的斜率和截距的最小二乘估计分别为

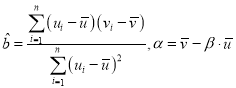
    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】执行如图所示的程序框图，当输入的的值为4时，输出的的值为2，则空白判断框中的条件可能为（ ）.

    A. B.

    C. D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆离心率为，点与椭圆的左、右顶点可以构成等腰直角三角形．点C是椭圆的下顶点，经过椭圆中心O的一条直线与椭圆交于A，B两个点（不与点C重合），直线CA，CB分别与x轴交于点D，E．

    （1）求椭圆的标准方程．

    （2）判断的大小是否为定值，并证明你的结论．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，.

    （1）讨论的单调性；

    （2）当时，若关于的不等式恒成立，求实数的取值范围.

    查看答案和解析>>

    同步练习册答案