
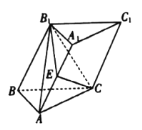
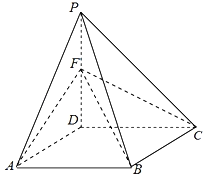
【题目】在斜三棱柱![]() 中,
中,![]() 为等腰直角三角形,
为等腰直角三角形,![]() ,平面
,平面![]() ⊥平面
⊥平面![]() ,点
,点![]() 为棱
为棱![]() 的中点,
的中点,![]() .
.
(1)证明:平面![]() 平面
平面![]() .
.
(2)求二面角![]() 的余弦值.
的余弦值.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)证明![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() 即得证;
即得证;
(2)由于![]() ,
,![]() ,
,![]() 两两垂直,以
两两垂直,以![]() 为坐标原点,
为坐标原点,![]() ,
,![]() ,
,![]() 分别为
分别为![]() ,
,![]() ,
,![]() 轴的正方向,建立如图所示的空间直角坐标系
轴的正方向,建立如图所示的空间直角坐标系![]() ,再利用向量法求出二面角
,再利用向量法求出二面角![]() 的余弦值.
的余弦值.
(1)证明:分别取![]() ,
,![]() 的中点
的中点![]() 和
和![]() ,连接
,连接![]() ,
,![]() ,
,![]() ,
,![]() .
.
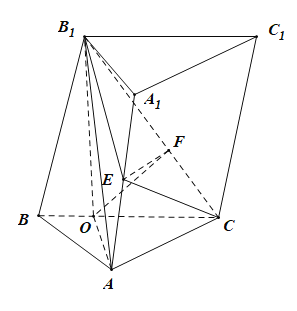
因为![]() ,
,![]() 为
为![]() 的中点,所以
的中点,所以![]() ,
,
因为平面![]() 平面
平面![]() ,且平面
,且平面![]() 平面
平面![]() .
.
所以![]() 平面
平面![]() ,
,
因为![]() 是
是![]() 的中点.
的中点.
所以![]() ,且
,且![]() ,
,
因为点![]() 为棱
为棱![]() 的中点所以
的中点所以![]() ,且
,且![]() ,
,
所以![]() ,且
,且![]() ,所以四边形
,所以四边形![]() 是平行四边形,则
是平行四边形,则![]() .
.
因为![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ,
,
因为![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() .
.
(2)由题意得![]() ,则
,则![]() 平面
平面![]() ,故
,故![]() ,
,![]() ,
,![]() 两两垂直.
两两垂直.
以![]() 为坐标原点,
为坐标原点,![]() ,
,![]() ,
,![]() 分别为
分别为![]() ,
,![]() ,
,![]() 轴的正方向,建立如图所示的空间直角坐标系
轴的正方向,建立如图所示的空间直角坐标系![]() ,
,
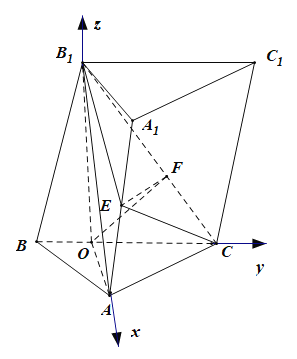
则![]() ,
,![]() ,
,![]() ,
,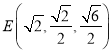 ,
,
故![]() ,
,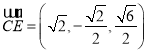 ,
,![]() ,
,
设平面![]() 的法向量为
的法向量为![]() ,
,
则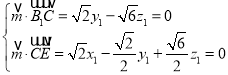 ,令
,令![]() ,得
,得![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,
,
则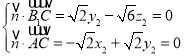 令
令![]() ,得
,得![]() ,
,
则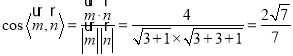 ,
,
由图可知二面角![]() 为锐角,则二面角
为锐角,则二面角![]() 的余弦值为
的余弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,底面ABCD是边长为2的菱形,∠DAB=60°,AD⊥PD,点F为棱PD的中点.
(1)在棱BC上是否存在一点E,使得CF∥平面PAE,并说明理由;
(2)若AC⊥PB,二面角D﹣FC﹣B的余弦值为![]() 时,求直线AF与平面BCF所成的角的正弦值.
时,求直线AF与平面BCF所成的角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】政府工作报告指出,2019年我国深入实施创新驱动发展战略,创新能力和效率进一步提升;2020年要提升科技支撑能力,健全以企业为主体的产学研一体化创新机制,某企业为了提升行业核心竞争力,逐渐加大了科技投入;该企业连续5年来的科技投入x(百万元)与收益y(百万元)的数据统计如下:
科技投入x | 1 | 2 | 3 | 4 | 5 |
收益y | 40 | 50 | 60 | 70 | 90 |
(1)请根据表中数据,建立y关于x的线性回归方程;
(2)按照(1)中模型,已知科技投入8百万元时收益为140百万元,求残差![]() (残差
(残差![]() 真实值-预报值).
真实值-预报值).
参考数据:回归直线方程![]() ,其中
,其中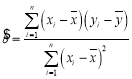 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在①![]() ;②
;②![]() ;③
;③![]()
![]() ,这三个条件中任选一个,补充在下面问题中,然后解答补充完整的题目.
,这三个条件中任选一个,补充在下面问题中,然后解答补充完整的题目.
在△![]() 中,内角A,B,C所对的边分别为
中,内角A,B,C所对的边分别为![]() .且满足_________.
.且满足_________.
(1)求![]() ;
;
(2)已知![]() ,△
,△![]() 的外接圆半径为
的外接圆半径为![]() ,求△
,求△![]() 的边AB上的高
的边AB上的高![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】质量是企业的生命线,某企业在一个批次产品中随机抽检![]() 件,并按质量指标值进行统计分析,得到表格如表:
件,并按质量指标值进行统计分析,得到表格如表:
质量指标值 | 等级 | 频数 | 频率 |
| 三等品 | 10 | 0.1 |
| 二等品 | 30 |
|
| 一等品 |
| 0.4 |
| 特等品 | 20 | 0.2 |
合计 |
| 1 | |
(1)求![]() ,
,![]() ,
,![]() ;
;
(2)从质量指标值在![]() 的产品中,按照等级分层抽样抽取6件,再从这6件中随机抽取2件,求至少有1件特等品被抽到的概率.
的产品中,按照等级分层抽样抽取6件,再从这6件中随机抽取2件,求至少有1件特等品被抽到的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若存在实常数![]() 和
和![]() ,使得函数
,使得函数![]() 和
和![]() 对其公共定义域上的任意实数x都满足:
对其公共定义域上的任意实数x都满足:![]() 和
和![]() 恒成立,则称此直线
恒成立,则称此直线![]() 为
为![]() 和
和![]() 的“隔离直线”,已知函数
的“隔离直线”,已知函数![]() ,
,![]() ,
,![]() (
(![]() 为自然对数的底数),则( )
为自然对数的底数),则( )
A.![]() 在
在![]() 内单调递增;
内单调递增;
B.![]() 和
和![]() 之间存在“隔离直线”,且
之间存在“隔离直线”,且![]() 的最小值为
的最小值为![]() ;
;
C.![]() 和
和![]() 之间存在“隔离直线”,且
之间存在“隔离直线”,且![]() 的取值范围是
的取值范围是![]() ;
;
D.![]() 和
和![]() 之间存在唯一的“隔离直线”
之间存在唯一的“隔离直线”![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com