
【题目】已知一个口袋内有4个不同的红球,6个不同的白球.
(1)从中任取4个球,红球的个数不比白球的个数少的取法有多少种?
(2)从中任取5个球,记取到红球的个数为X,求X的分布列和数学期望.
【答案】(1)115;(2)见解析
【解析】
(1)由题意知本题是一个分类计数问题,取4个红球,没有白球,有C44种,取3个红球1个白球,有C43C61种;取2个红球2个白球,有C42C62,根据加法原理得到结果;
(2) 令取到红球的个数为X,则X的可能取值为0,1,2,3,4,分别求出相应的概率,由此能求出X的分布列和数学期望.
(1)将取出4个球分成三类情况:①取4个红球,没有白球,有![]() 种取法;②取3个红球、1个白球,有
种取法;②取3个红球、1个白球,有![]() 种取法;③取2个红球、2个白球,有
种取法;③取2个红球、2个白球,有![]() 种取法.
种取法.
根据分类加法计数原理,共有取法![]() +
+![]() +
+![]() =115(种).
=115(种).
(2)X的可能取值为0,1,2,3,4,对应的概率分别为P(X=0)=![]() =
=![]() ,P(X=1)=
,P(X=1)=![]() =
=![]() ,P(X=2)=
,P(X=2)=![]() =
=![]() ,P(X=3)=
,P(X=3)=![]() =
=![]() ,P(X=4)=
,P(X=4)=![]() =
=![]() .
.
所以X的分布列为
X | 0 | 1 | 2 | 3 | 4 |
P |
|
|
|
|
|
所以E(X)=0×![]() +1×
+1×![]() +2×
+2×![]() +3×
+3×![]() +4×
+4×![]() =1.
=1.


科目:高中数学 来源: 题型:
【题目】已知数列{an}与{bn}满足an=2bn+3(n∈N*),若{bn}的前n项和为Sn= ![]() (3n﹣1)且λan>bn+36(n﹣3)+3λ对一切n∈N*恒成立,则实数λ的取值范围是 .
(3n﹣1)且λan>bn+36(n﹣3)+3λ对一切n∈N*恒成立,则实数λ的取值范围是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】记实数x1 , x2 , …,xn中最小数为min{x1 , x2 , …,xn},则定义在区间[0,+∞)上的函数f(x)=min{x2+1,x+3,13﹣x}的最大值为( )
A.5
B.6
C.8
D.10
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱ABC﹣A1B1C1中,侧棱垂直于底面,∠BAC=90°,AB=AA1=2,AC=1,点M和N分别为A1B1和BC的中点.
(1)求证:AC⊥BM;
(2)求证:MN∥平面ACC1A1;
(3)求二面角M﹣BN﹣A的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为2,O为AD的中点,射线OP从OA出发,绕着点O顺时针方向旋转至OD,在旋转的过程中,记∠AOP为x(x∈[0,π]),OP所经过正方形ABCD内的区域(阴影部分)的面积S=f(x),那么对于函数f(x)有以下三个结论:
①f( ![]() )=
)= ![]() ;
;
②任意x∈[0, ![]() ],都有f(
],都有f( ![]() ﹣x)+f(
﹣x)+f( ![]() +x)=4;
+x)=4;
③任意x1 , x2∈( ![]() ,π),且x1≠x2 , 都有
,π),且x1≠x2 , 都有 ![]() <0.
<0.
其中所有正确结论的序号是 . 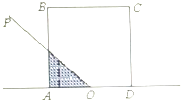
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某班有50名学生,一次考试后数学成绩ξ~N(110,102),若P(100≤ξ≤110)=0.34,则估计该班学生数学成绩在120分以上的人数为 ( )
A. 10 B. 9 C. 8 D. 7
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某调查机构观察了某地100个新生婴儿的体重,并根据所得数据画出了样本的频率分布直方图如图,则新生婴儿的体重在[3.2,4.0)(kg)的有人.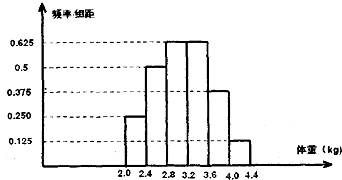
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com