
分析 设第十名到第一名得到的奖金分别是a1,a2,…,a10,则an=$\frac{1}{2}$Sn+1,可证奖金数组成一个以2为首项,公比为2的等比数列,由等比数列的求和公式可得.
解答 解:设第十名到第一名得到的奖金分别是a1,a2,…,a10,
则an=$\frac{1}{2}$Sn+1,∴a1=2,an-an-1=$\frac{1}{2}$an,∴an=2an-1
∴每人所得奖金数组成一个以2为首项,公比为2的等比数列,
∴S10=$\frac{2×(1-{2}^{10})}{1-2}$=2046
∴此科研单位共拿出2046万元资金进行奖励.
点评 本题考查等比数列的求和公式,构造并判断数列为等比数列是解决问题的关键,属中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | t∉M | B. | t+2∈M | C. | t+1∈M | D. | t-1∉M |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{12}$或$\frac{5π}{12}$ | B. | $\frac{π}{6}$或$\frac{π}{3}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | 1 | C. | 2 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | .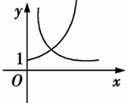 | B. | .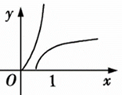 | C. | .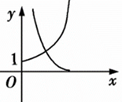 | D. | .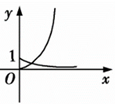 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com