练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知数列的前项和为，且.

    （1）求数列的通项公式；

    （2）设，数列的前项和为，求使不等式对一切都成立的正整数的最大值.

    （3）设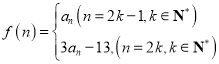，是否存在，使得成立?若存在，求出的值；若不存在，请说明理由.

    【答案】（1）（2）672（3）不存在，理由见解析

    【解析】

    （1）由数列的递推式，计算可得所求通项公式；

    （2）求得，运用裂项相消求和可得，判断的单调性，可得最小值，即可得到的最大值；

    （3）讨论为奇数或偶数，假设存在，计算可判断是否存在．

    解：（1）因为，所以，又因为满足上式，所以.

    （2）由（1）可知，所以，显然随着的增大而增大，故的最小值为，由可得.

    （3）结论：不存在满足条件的.

    理由如下:①当为奇数时为偶数，则，即，所以，解得，矛盾.

    ②当为偶数时为奇数，则，即，所以，解得，矛盾.综上所述，不存在满足条件的.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知矩阵.

    （1）求直线在对应的变换作用下所得的曲线方程；

    （2）求矩阵的特征值与特征向量.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设a，b，c为实数，f（x）=（x+a）（x2+bx+c），g（x）=（ax+1）（cx2+bx+1）．记集合S={x|f（x）=0，x∈R}，T={x|g（x）=0，x∈R}．若{S}，{T}分别为集合S，T 的元素个数，则下列结论不可能的是（ ）

    A.{S}=1且{T}=0B.{S}=1且{T}=1C.{S}=2且{T}=2D.{S}=2且{T}=3

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数， ．

    （1）讨论函数的单调性；

    （2）当时， 恒成立，求实数的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】为缓解堵车现象，解决堵车问题，银川市交警队调查了甲乙两个路口的车流量，在2019年6月随机选取了14天，统计每天上午7：30-9：00早高峰时段各自的车流量（单位：百辆）得到如图所示的茎叶图，根据茎叶图回答以下问题.

    （1）甲乙两个路口的车流量的中位数分别是多少?

    （2）试计算甲乙两个路口的车流量在之间的频率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知样本

    10.1

    8.7

    6.4

    10.5

    13.0

    8.3

    10.0

    12.4

    8.0

    9.0

    11.2

    9.3

    12.7

    9.6

    10.6

    11.0

    那么其分位数和分位数分别是（ ）

    A.和B.和C.和D.和

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】中国古代数学著作《算法统综》中有这样的一个问题：“三百七十八里关，初步健步不为难，次日脚痛减一半，六朝才得到其关，要见次日行里数，请公仔细算相还”.其大意为：“有一个人走378里路，第一天健步行走，从第二天起脚痛每天走的路程为前一天的一半，走了6天后到达目的地”，请问此人第2天走的路程为

    A. 24里 B. 48里 C. 72里 D. 96里

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】正项数列的前项和为，且.

    （Ⅰ）试求数列的通项公式；

    （Ⅱ）设，求的前项和为.

    （Ⅲ）在（Ⅱ）的条件下，若对一切恒成立，求实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数=，其中a>0,且a≠1

    (1)判断的奇偶性，并证明你的结论;

    (2)若关于的不等式≤||在[﹣1,1]上恒成立,求实数a的取值范围

    查看答案和解析>>

    同步练习册答案