
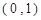 的随机数,则斜边的长小于
的随机数,则斜边的长小于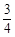 的概率为 。
的概率为 。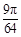
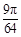 ,题目即求它与边长为1的正方行面积的比P=
,题目即求它与边长为1的正方行面积的比P=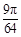 ,故答案为
,故答案为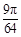


 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
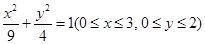 ,为估计椭圆
,为估计椭圆 的面积,现采用随机模拟方式产生
的面积,现采用随机模拟方式产生 的200个点
的200个点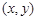 ,经统计,落在图中阴影部分的点共157个,则可估计椭圆
,经统计,落在图中阴影部分的点共157个,则可估计椭圆 的面积是 .(精确到0.01)
的面积是 .(精确到0.01)
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
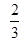 ,则阴影区域的面积为( )
,则阴影区域的面积为( ) 
A.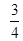 | B.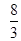 | C.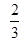 | D.无法计算 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
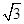 为半径画一弧,分别交AB,AC于D,E.若在△ABC这一平面区域内任丢一粒豆子,则豆子落在扇形ADE内的概率是________.
为半径画一弧,分别交AB,AC于D,E.若在△ABC这一平面区域内任丢一粒豆子,则豆子落在扇形ADE内的概率是________.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
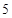 米的绳子,拉直后在任意位置剪断,则剪得两段的长度都不小于1米,且以剪得的两段绳为两边的矩形的面积都不大于
米的绳子,拉直后在任意位置剪断,则剪得两段的长度都不小于1米,且以剪得的两段绳为两边的矩形的面积都不大于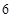 平方米的概率为( )
平方米的概率为( )A.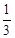 | B.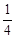 | C.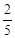 | D.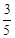 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com