
【题目】已知f(x)=4sinωxsin(ωx+ ![]() )﹣1(ω>0),f(x)的最小正周期为π. (Ⅰ)当x∈[0,
)﹣1(ω>0),f(x)的最小正周期为π. (Ⅰ)当x∈[0, ![]() ]时,求f(x)的最大值;
]时,求f(x)的最大值;
(Ⅱ)请用“五点作图法”画出f(x)在[0,π]上的图象.
【答案】解:(Ⅰ)由f(x)=4sinωxsin(ωx+ ![]() )﹣1=2sin2ωx﹣1+2
)﹣1=2sin2ωx﹣1+2 ![]() sinωxcosωx=2sin(2ωx﹣
sinωxcosωx=2sin(2ωx﹣ ![]() ) 由f(x)的最小正周期为π,得ω=1,所以f(x)=2sin(2x﹣
) 由f(x)的最小正周期为π,得ω=1,所以f(x)=2sin(2x﹣ ![]() ).
).
因为x∈[0, ![]() ],所以2x﹣
],所以2x﹣ ![]() ∈[﹣
∈[﹣ ![]() ,
, ![]() ],
],
故当2x﹣ ![]() =
= ![]() ,即x=
,即x= ![]() 时,f(x)取得最大值2.
时,f(x)取得最大值2.
(Ⅱ)由f(x)=2sin(2ωx﹣ ![]() )知:
)知:
2x﹣ | ﹣ | 0 |
| π |
|
|
x | 0 |
|
|
|
| π |
f(x) | ﹣1 | 0 | 2 | 0 | ﹣2 | ﹣1 |
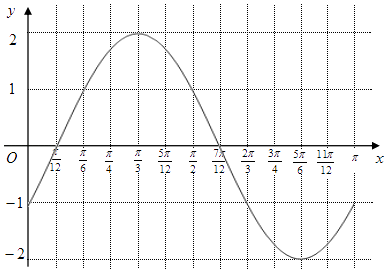
【解析】(Ⅰ)先化简f(x),由周期可求ω,从而得f(x)解析式,再根据函数性质求出f(x)的最大值(Ⅱ)用“五点法”可得f(x)的图象,注意x的范围
【考点精析】本题主要考查了五点法作函数y=Asin(ωx+φ)的图象的相关知识点,需要掌握描点法及其特例—五点作图法(正、余弦曲线),三点二线作图法(正、余切曲线)才能正确解答此题.


 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案科目:高中数学 来源: 题型:
【题目】一位网民在网上光顾某网店,经过一番浏览后,对该店铺中的A,B,C三种商品有购买意向.已知该网民购买A种商品的概率为 ![]() ,购买B种商品的槪率为
,购买B种商品的槪率为 ![]() ,购买C种商品的概率为
,购买C种商品的概率为 ![]() .假设该网民是否购买这三种商品相互独立
.假设该网民是否购买这三种商品相互独立
(1)求该网民至少购买2种商品的概率;
(2)用随机变量η表示该网民购买商品的种数,求η的槪率分布和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a>0,a≠1且loga3>loga2,若函数f(x)=logax在区间[a,2a]上的最大值与最小值之差为1.
(1)求a的值;
(2)解不等式 ![]() ;
;
(3)求函数g(x)=|logax﹣1|的单调区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设 ![]() ,曲线y=f(x)在点(1,f(1))处的切线与直线2x+y+1=0垂直.
,曲线y=f(x)在点(1,f(1))处的切线与直线2x+y+1=0垂直.
(1)求a的值;
(2)若x∈[1,+∞),f(x)≤m(x﹣1)恒成立,求m的范围.
(3)求证: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
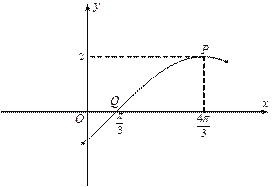
【题目】如图为函数![]() 图像的一部分,其中点
图像的一部分,其中点![]() 是图像的一个最高点,点
是图像的一个最高点,点![]() 是与点
是与点![]() 相邻的图像与
相邻的图像与![]() 轴的一个交点.
轴的一个交点.
⑴ 求函数![]() 的解析式;
的解析式;
⑵ 若将函数![]() 的图像沿
的图像沿![]() 轴向右平移
轴向右平移![]() 个单位,再把所得图像上每一点的横坐标都变为原来的
个单位,再把所得图像上每一点的横坐标都变为原来的![]() (纵坐标不变),得到函数
(纵坐标不变),得到函数![]() 的图像,求函数
的图像,求函数![]() 的单调递增区间.
的单调递增区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近几年,电商行业的蓬勃发展也带动了快递业的高速发展.某快递配送站每天至少要完成1800件包裹的配送任务,该配送站有8名新手快递员和4名老快递员,但每天最多安排10人进行配送.已知每个新手快递员每天可配送240件包裹,日工资320元;每个老快递员每天可配送300件包裹,日工资520元.
(1)求该配送站每天需支付快递员的总工资最小值;
(2)该配送站规定:新手快递员某个月被评为“优秀”,则其下个月的日工资比这个月提高12%.那么新手快递员至少连续几个月被评为“优秀”,日工资会超过老快递员?
(参考数据: ![]() ,
, ![]() ,
, ![]() .)
.)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正方体ABCD﹣A1B1C1D1中,M、N分别为棱C1D1、C1C的中点,有以下四个结论: ①直线AM与CC1是相交直线;
②直线AM与BN是平行直线;
③直线BN与MB1是异面直线;
④直线AM与DD1是异面直线.
其中正确的结论为(注:把你认为正确的结论的序号都填上).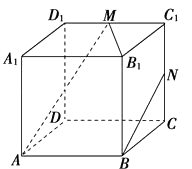
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)的定义域为R,f(x)= ![]() ,且对任意的x∈R都有f(x+1)=﹣
,且对任意的x∈R都有f(x+1)=﹣ ![]() ,若在区间[﹣5,1]上函数g(x)=f(x)﹣mx+m恰有5个不同零点,则实数m的取值范围是( )
,若在区间[﹣5,1]上函数g(x)=f(x)﹣mx+m恰有5个不同零点,则实数m的取值范围是( )
A.[﹣ ![]() ,﹣
,﹣ ![]() )
)
B.(﹣ ![]() ,﹣
,﹣ ![]() ]
]
C.(﹣ ![]() ,0]
,0]
D.(﹣ ![]() ,﹣
,﹣ ![]() ]
]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某理科考生参加自主招生面试,从7道题中(4道理科题3道文科题)不放回地依次任取3道作答.
(1)求该考生在第一次抽到理科题的条件下,第二次和第三次均抽到文科题的概率;
(2)规定理科考生需作答两道理科题和一道文科题,该考生答对理科题的概率均为![]() ,答对文科题的概率均为
,答对文科题的概率均为![]() ,若每题答对得10分,否则得零分.现该生已抽到三道题(两理一文),求其所得总分
,若每题答对得10分,否则得零分.现该生已抽到三道题(两理一文),求其所得总分![]() 的分布列与数学期望
的分布列与数学期望![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com