
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() :
:![]() 与直线
与直线![]() (
(![]() )交于
)交于![]() ,
,![]() 两点.
两点.
(1)当![]() 时,分别求
时,分别求![]() 在点
在点![]() 和
和![]() 处的切线方程;
处的切线方程;
(2)![]() 轴上是否存在点
轴上是否存在点![]() ,使得当
,使得当![]() 变动时,总有
变动时,总有![]() ?说明理由.
?说明理由.
科目:高中数学 来源: 题型:
【题目】为了解学生身高情况,某校以10%的比例对全校700名学生按性别进行分层抽样调查,测得身高情况的统计图如下:
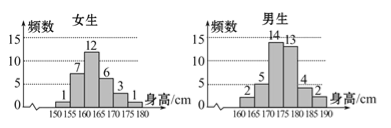
(1)估计该校男生的人数;
(2)估计该校学生身高在170~185cm之间的概率;
(3)从样本中身高在180~190cm之间的男生中任选2人,求至少有1人身高在185~190cm之间的概率。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,
中,![]() 底面
底面![]() ,底面
,底面![]() 是直角梯形,
是直角梯形,![]() ,
,![]() 是
是![]() 上的点.
上的点.
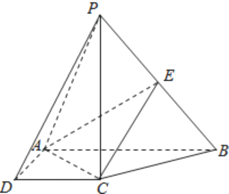
(1)求证: 平面![]() 平面
平面![]() ;
;
(2)若![]() 是
是![]() 的中点,且二面角
的中点,且二面角![]() 的余弦值为
的余弦值为![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】众所周知,乒乓球是中国的国球,乒乓球队内部也有着很严格的竞争机制,为了参加国际大赛,种子选手甲与三位非种子选手乙、丙、丁分别进行一场内部对抗赛,按以往多次比赛的统计,甲获胜的概率分别为![]() ,
,![]() ,
,![]() ,且各场比赛互不影响.
,且各场比赛互不影响.
(1)若甲至少获胜两场的概率大于![]() ,则甲入选参加国际大赛参赛名单,否则不予入选,问甲是否会入选最终的大名单?
,则甲入选参加国际大赛参赛名单,否则不予入选,问甲是否会入选最终的大名单?
(2)求甲获胜场次![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设不等式组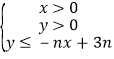 所表示的平面区域为
所表示的平面区域为![]() ,记
,记![]() 内的整点个数为
内的整点个数为![]() ,(整点即横、纵坐标均为整数的点)
,(整点即横、纵坐标均为整数的点)
(1)计算![]() 的值;
的值;
(2)求数列![]() 的通项公式
的通项公式![]() ;
;
(3)记数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() ,若对于一切的正整数
,若对于一切的正整数![]() ,总有
,总有![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某次测量中得到的A样本数据如下:82,84,84,86,86,86,88,88,88,88,若样本B数据恰好是样本A数据都加上2后所得数据,则A,B两样本的下列数字特征对应相同的是( )
A. 众数 B. 平均数
C. 中位数 D. 标准差
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com