
【题目】某城市100户居民的月平均用电量(单位:度),以![]() 分组的频率分布直方图如图所示.
分组的频率分布直方图如图所示.

(1)求直方图中![]() 的值;
的值;
(2)求月平均用电量的众数和中位数;
(3)在月平均用电量为![]() 的四组用户中,用分层抽样的方法抽取11户居民,则月平均用电量在
的四组用户中,用分层抽样的方法抽取11户居民,则月平均用电量在![]() 的用户中应抽取多少户?
的用户中应抽取多少户?
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
试题分析:(1)通过已知高的矩形面积和所有矩形的面积和为![]() ,求出未知高的一组的概率,除以底边长即得
,求出未知高的一组的概率,除以底边长即得![]() 的值;(2)频率分布直方图中频率最高的一组的中点为众数,中位数是频率为
的值;(2)频率分布直方图中频率最高的一组的中点为众数,中位数是频率为![]() 的分界点;(3)根据频率分布直方图求出
的分界点;(3)根据频率分布直方图求出![]() 四组的户数,根据分层抽样的规则:按它们在总体中所占比例抽取即可.
四组的户数,根据分层抽样的规则:按它们在总体中所占比例抽取即可.
试题解析:(1)由![]() 得:
得:![]() ,
,
所以直方图中![]() 的值是0.0075.
的值是0.0075.
(2)月平均用电量的众数为![]() ,
,
![]() ,
,
∴月平均用电量的中位数在![]() 内,设中位数为
内,设中位数为![]() ,由
,由![]() ,得
,得![]() .
.
即月平均用电量的中位数为224.
(3)月平均用电量为![]() 的用户有
的用户有![]() 户,用平均用电量为
户,用平均用电量为![]() 的用户有
的用户有![]() 户,用平均用电量为
户,用平均用电量为![]() 的用户有
的用户有![]() 户,用平均用电量为
户,用平均用电量为![]() 的用户有
的用户有![]() 户,抽取比例为
户,抽取比例为![]() ,
,
∴用平均用电量为![]() 的用户中应抽取
的用户中应抽取![]() 户.
户.


科目:高中数学 来源: 题型:
【题目】在某次测验中,有6位同学的平均成绩为75分, 用xn表示编号为n(n=1,2,…,6)的同学所得成绩,且前5位同学的成绩如下:
编号n | 1 | 2 | 3 | 4 | 5 |
成绩xn | 70 | 76 | 72 | 70 | 72 |
(1)求第6位同学的成绩x6,及这6位同学成绩的标准差s;
(2)从前5位同学中选2位同学,求恰有1位同学成绩在区间(68,75)中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)求过直线l1:x-2y+3=0与直线l2:2x+3y-8=0的交点,且到点P(0,4)的距离为2的直线方程.
(2)设直线l的方程为(a+1)x+y+2-a=0(a∈R).若l在两坐标轴上的截距相等,求l的方程;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知棱长为l的正方体![]() 中,E,F,M分别是AB、AD、
中,E,F,M分别是AB、AD、![]() 的中点,又P、Q分别在线段
的中点,又P、Q分别在线段![]() 上,且
上,且![]() ,设面
,设面![]() 面MPQ=
面MPQ=![]() ,则下列结论中不成立的是( )
,则下列结论中不成立的是( )

A.![]() 面ABCD
面ABCD
B.![]() AC
AC
C.面MEF与面MPQ不垂直
D.当x变化时,![]() 不是定直线
不是定直线
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高校调查了20名学生每周的自习时间(单位:小时),制成了如图所示的频率分布直方图,其中自习时间的范围是![]() ,样本数据分组为
,样本数据分组为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.

(1)求直方图中![]() 的值;
的值;
(2)从每周自习时间在![]() 的受调查学生中,随机抽取2人,求恰有1人的每周自习时间在
的受调查学生中,随机抽取2人,求恰有1人的每周自习时间在![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
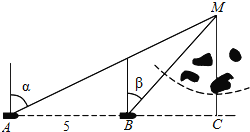
【题目】如图,一船由西向东航行,在A处测得某岛M的方位角为α,前进5km后到达B处,测得岛M的方位角为β.已知该岛周围3km内有暗礁,现该船继续东行.
(1)若α=2β=60°,问该船有无触礁危险?
(2)当α与β满足什么条件时,该船没有触礁的危险?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为迎接春节,某工厂大批生产小孩具—— 拼图,工厂为了规定工时定额,需要确定加工拼图所花费的时间,为此进行了10次试验,测得的数据如下:
拼图数
| 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 |
加工时间
| 62 | 68 | 75 | 81 | 89 | 95 | 102 | 108 | 115 | 122 |
(1)画出散点图,并判断![]() 与
与![]() 是否具有线性相关关系;
是否具有线性相关关系;

(2)求回归方程;
(3)根据求出的回归方程,预测加工2010个拼图需要用多少小时?(精确到0.1)
附:回归直线的斜率和截距的最小二乘估计公式分别为:
 ,
, ![]() .
.
参考数据 | 合计 | ||||||||||
| 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 | 550 |
| 62 | 68 | 75 | 81 | 89 | 95 | 102 | 108 | 115 | 122 | 917 |
| 100 | 400 | 900 | 1600 | 2500 | 3600 | 4900 | 6400 | 8100 | 10000 | 38500 |
| 620 | 1360 | 2250 | 3240 | 4450 | 5700 | 7140 | 8840 | 10350 | 12200 | 55950 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com