练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    18．已知集合P={-1，0，1}，$Q=\left\{{x\left|{y=\sqrt{x+1}}\right.}\right\}$，则P∩Q=（　　）
    A．PB．QC．{-1，1}D．{0，1}

    分析 先分别求出集合P和Q，由此利用交集定义能出P∩Q．

    解答 解：∵集合P={-1，0，1}，
    $Q=\left\{{x\left|{y=\sqrt{x+1}}\right.}\right\}$={x|x≥-1}，
    ∴P∩Q={-1，0，1}=P．
    故选：A．

    点评 本题考查交集的求法，是基础题，解题时要认真审题，注意交集定义的合理运用．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

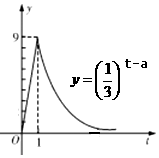    8．我国科研人员屠呦呦发现从青篙中提取的青篙素抗疟性超强，几乎达到100%，据监测：服药后每毫升血液中的含药量y（微克）与时间t（小时）之间近似满足如图所示的曲线．
    （1）写出第一次服药后y与t之间的函数关系式y=f（t）；
    （2）据进一步测定：每毫升血液中含药量不少于$\frac{1}{9}$微克时，治疗有效，求服药一次后治疗有效的时间是多长？

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    9．已知双曲线${C_1}：\frac{x^2}{a^2}-\frac{y^2}{b^2}=1（{a＞0，b＞0}）$与圆${C_2}：{x^2}+{y^2}={c^2}$（c是双曲线的半焦距）相交于第一象限内一点P，又F1，F2分别是双曲线C1的左、右焦点，若$∠P{F_2}{F_1}=\frac{π}{3}$，则双曲线的离心率为$\sqrt{3}+1$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    6．若数列{an}满足$\frac{1}{{a}_{n+1}}$-$\frac{1}{{a}_{n}}$=d（n∈N*，d为常数），则称数列{an}为调和数列，现有一调和数列{bn}满足b1=1，b2=$\frac{1}{2}$．
    （1）求{bn}的通项公式；
    （2）若数列cn=$\frac{{b}_{n}}{n+2}$，求{cn}的前n项和Sn．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    13．已知函数f（x）=ax-k的图象过点（1，3）和（0，2），则函数f（x）的解析式为f（x）=2x+1．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    3．如图，四边形ABCD为菱形，G为AC与BD的交点，BE⊥平面ABCD．
    （1）证明：平面AEC⊥平面BED．
    （2）若∠ABC=120°，AE⊥EC，AB=2，求点G到平面AED的距离．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    10．已知由甲、乙两位男生和丙、丁两位女生组成的四人冲关小组，参加由安徽卫视推出的大型户外竞技类活动《男生女生向前冲》，活动共有四关，设男生闯过一至四关的概率依次是$\frac{5}{6}，\frac{4}{5}，\frac{3}{4}，\frac{2}{3}$，女生闯过一至四关的概率依次是$\frac{4}{5}，\frac{3}{4}，\frac{2}{3}，\frac{1}{2}$．
    （1）求男生闯过四关的概率；
    （2）设ε表示四人冲关小组闯过四关的人数，求随机变量?的分布列和期望．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    7．为迎接春节，某工厂大批生产小孩玩具--拼图，工厂为了规定工时定额，需要确定加工拼图所花费的时间，为此进行了5次试验，测得的数据如下：
    拼图数x/个1020304050
    加工时间y/分钟6268758189
    （1）画出散点图，并判断y与x是否具有相关关系；
    （2）求回归方程；
    （3）根据求出的回归方程，预测加工2 00个拼图需用多少分钟．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    8．已知函数f（x）=sinx．
    （1）当x＞0时，证明：${f^'}（x）＞1-\frac{x^2}{2}$；
    （2）若当$x∈（0，\frac{π}{2}）$时，$f（x）+\frac{f（x）}{{{f^'}（x）}}＞ax$恒成立，求实数a的取值范围．

    查看答案和解析>>

    同步练习册答案