
【题目】已知函数![]() ,
,![]() .
.
(1)求证:![]() 在区间
在区间![]() 上无零点;
上无零点;
(2)求证:![]() 有且仅有2个零点.
有且仅有2个零点.
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:高中数学 来源: 题型:
【题目】已知曲线![]() 的参数方程为
的参数方程为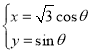 (
(![]() 为参数),在同一平面直角坐标系中,将曲线
为参数),在同一平面直角坐标系中,将曲线![]() 上的点按坐标变换
上的点按坐标变换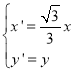 得到曲线
得到曲线![]() ,以原点为极点,
,以原点为极点,![]() 轴的正半轴为极轴,建立极坐标系.设
轴的正半轴为极轴,建立极坐标系.设![]() 点的极坐标为
点的极坐标为![]() .
.
(1)求曲线![]() 的极坐标方程;
的极坐标方程;
(2)若过点![]() 且倾斜角为
且倾斜角为![]() 的直线
的直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.

(1)求证:平面![]() 平面
平面![]() ;
;
(2)在线段![]() 上是否存在点
上是否存在点![]() ,使得平面
,使得平面![]() 与平面
与平面![]() 所成锐二面角为
所成锐二面角为![]() ?若存在,求
?若存在,求![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】PM2.5是空气质量的一个重要指标,我国PM2.5标准采用世卫组织设定的最宽限值,即PM2.5日均值在35μg/m3以下空气质量为一级,在35μg/m3~75μg/m3之间空气质量为二级,在75μg/m3以上空气质量为超标.如图是某市2019年12月1日到10日PM2.5日均值(单位:μg/m3)的统计数据,则下列叙述不正确的是( )
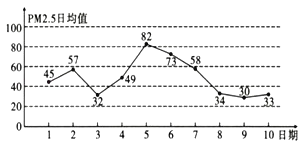
A.这10天中,12月5日的空气质量超标
B.这10天中有5天空气质量为二级
C.从5日到10日,PM2.5日均值逐渐降低
D.这10天的PM2.5日均值的中位数是47
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将6名党员干部分配到4个贫困村驻村扶贫,每个贫困村至少分配1名党员干部,则不同的分配方案共有( )
A.2640种B.4800种C.1560种D.7200种
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的是( )
A. 命题“若![]() ,则
,则![]() ”的否命题是“若
”的否命题是“若![]() ,则
,则![]() ”
”
B. 命题“![]() ,
,![]() ”的否定是“
”的否定是“![]() ,
,![]() ”
”
C. “![]() 在
在![]() 处有极值”是“
处有极值”是“![]() ”的充要条件
”的充要条件
D. 命题“若函数![]() 有零点,则“
有零点,则“![]() 或
或![]() ”的逆否命题为真命题
”的逆否命题为真命题
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着“互联网+交通”模式的迅猛发展,“共享自行车”在很多城市相继出现。某运营公司为了了解某地区用户对其所提供的服务的满意度,随机调查了40个用户,得到用户的满意度评分如下:
用户编号 | 评分 | 用户编号 | 评分 | 用户编号 | 评分 | 用户编号 | 评分 | |||
1 2 3 4 5 6 7 8 9 10 | 78 73 81 92 95 85 79 84 63 86 | 11 12 13 14 15 16 17 18 19 20 | 88 86 95 76 97 78 88 82 76 89 | 21 22 23 24 25 26 27 28 29 30 | 79 83 72 74 91 66 80 83 74 82 | 31 32 33 34 35 36 37 38 39 40 | 93 78 75 81 84 77 81 76 85 89 |
用系统抽样法从40名用户中抽取容量为10的样本,且在第一分段里随机抽到的评分数据为92.
(1)请你列出抽到的10个样本的评分数据;
(2)计算所抽到的10个样本的均值![]() 和方差
和方差![]() ;
;
(3)在(2)条件下,若用户的满意度评分在![]() 之间,则满意度等级为“
之间,则满意度等级为“![]() 级”。试应用样本估计总体的思想,根据所抽到的10个样本,估计该地区满意度等级为“
级”。试应用样本估计总体的思想,根据所抽到的10个样本,估计该地区满意度等级为“![]() 级”的用户所占的百分比是多少?
级”的用户所占的百分比是多少?
(参考数据:![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,椭圆![]() :
:![]() (
(![]() )和圆
)和圆![]() :
:![]() ,已知圆
,已知圆![]() 将椭圆
将椭圆![]() 的长轴三等分,椭圆
的长轴三等分,椭圆![]() 右焦点到右准线的距离为
右焦点到右准线的距离为![]() ,椭圆
,椭圆![]() 的下顶点为
的下顶点为![]() ,过坐标原点
,过坐标原点![]() 且与坐标轴不重合的任意直线
且与坐标轴不重合的任意直线![]() 与圆
与圆![]() 相交于点
相交于点![]() 、
、![]() .
.

(1)求椭圆![]() 的方程;
的方程;
(2)若直线![]() 、
、![]() 分别与椭圆
分别与椭圆![]() 相交于另一个交点为点
相交于另一个交点为点![]() 、
、![]() .
.
①求证:直线![]() 经过一定点;
经过一定点;
②试问:是否存在以![]() 为圆心,
为圆心,![]() 为半径的圆
为半径的圆![]() ,使得直线
,使得直线![]() 和直线
和直线![]() 都与圆
都与圆![]() 相交?若存在,请求出实数
相交?若存在,请求出实数![]() 的范围;若不存在,请说明理由。
的范围;若不存在,请说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com