
【题目】某地区今年1月,2月,3月患某种传染病的人数分别为42,48,52.为了预测以后各月的患病人数,甲选择了模型![]() ,乙选择了模型
,乙选择了模型![]() ,其中
,其中![]() 为患病人数,
为患病人数,![]() 为月份数,a,b,c,p,q,r都是常数.结果4月,5月,6月份的患病人数分别为54,57,58.
为月份数,a,b,c,p,q,r都是常数.结果4月,5月,6月份的患病人数分别为54,57,58.
(1)求a,b,c,p,q,r的值;
(2)你认为谁选择的模型好.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2x![]() ,g(x)=(4﹣lnx)lnx+b(b∈R).
,g(x)=(4﹣lnx)lnx+b(b∈R).
(1)若f(x)>0,求实数x的取值范围;
(2)若存在x1,x2∈[1,+∞),使得f(x1)=g(x2),求实数b的取值范围;
查看答案和解析>>
科目:高中数学 来源: 题型:
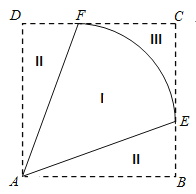
【题目】某地拟规划种植一批芍药,为了美观,将种植区域(区域I)设计成半径为1km的扇形![]() ,中心角
,中心角![]() (
(![]() ).为方便观赏,增加收入,在种植区域外围规划观赏区(区域II)和休闲区(区域III),并将外围区域按如图所示的方案扩建成正方形
).为方便观赏,增加收入,在种植区域外围规划观赏区(区域II)和休闲区(区域III),并将外围区域按如图所示的方案扩建成正方形![]() ,其中点
,其中点![]() ,
,![]() 分别在边
分别在边![]() 和
和![]() 上.已知种植区、观赏区和休闲区每平方千米的年收入分别是10万元、20万元、20万元.
上.已知种植区、观赏区和休闲区每平方千米的年收入分别是10万元、20万元、20万元.
(1)要使观赏区的年收入不低于5万元,求![]() 的最大值;
的最大值;
(2)试问:当![]() 为多少时,年总收入最大?
为多少时,年总收入最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某支上市股票在30天内每股的交易价格![]() (单位:元)与时间
(单位:元)与时间![]() (单位:天)组成有序数对
(单位:天)组成有序数对![]() ,点
,点![]() 落在如图所示的两条线段上.该股票在30天内(包括30天)的日交易量
落在如图所示的两条线段上.该股票在30天内(包括30天)的日交易量![]() (单位:万股)与时间
(单位:万股)与时间![]() (单位:天)的部分数据如下表所示:
(单位:天)的部分数据如下表所示:
第 | 4 | 10 | 16 | 22 |
| 36 | 30 | 24 | 18 |

(Ⅰ)根据所提供的图象,写出该种股票每股的交易价格![]() 与时间
与时间![]() 所满足的函数解析式;
所满足的函数解析式;
(Ⅱ)根据表中数据确定日交易量![]() 与时间
与时间![]() 的一次函数解析式;
的一次函数解析式;
(Ⅲ)若用![]() (万元)表示该股票日交易额,请写出
(万元)表示该股票日交易额,请写出![]() 关于时间
关于时间![]() 的函数解析式,并求出在这30天中,第几天的日交易额最大,最大值是多少?
的函数解析式,并求出在这30天中,第几天的日交易额最大,最大值是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() ,圆
,圆![]() ,动圆
,动圆![]() 与圆
与圆![]() 外切并且与圆
外切并且与圆![]() 内切,圆心
内切,圆心![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)过点![]()
![]() 作圆
作圆![]() 的两条切线,切点分别为
的两条切线,切点分别为![]() ,求直线
,求直线![]() 被曲线
被曲线![]() 截得的弦的中点坐标.
截得的弦的中点坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解本市居民的生活成本,甲乙丙三名同学利用假期分别对三个社区进行了“家庭每月日常消费额”的调查.他们将调查所得的数据分别绘制成频率分布直方图(如图所示),记甲乙丙所调查数据的标准差分别为![]() ,
,![]() ,
,![]() ,则它们的大小关系为__________.
,则它们的大小关系为__________.

(甲)

(乙)

(丙)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知整数对排列如下:(1,1),(1,2),(2,1),(1,3),(2,2),(3,1),(1,4),(2,3),(3,2),(4,1),(1,5),(2,4)......则第60个整数对是( )
A.(5,7)B.(11,5)C.(7,5)D.(5,11)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com