
已知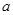 为常数,则使得
为常数,则使得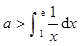 成立的一个充分而不必要条件是 ( )
成立的一个充分而不必要条件是 ( )
A.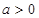 B.
B.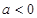 C.
C.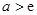 D.
D.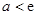
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:高中数学 来源: 题型:
. |
| x\~(a1)(a2)(a3)…(an-1)(an) |
. |
| 2\~(-1)(3)(-2)(1) |
| 1 |
| 1-ak |
. |
| 2\~(a1)(a2)(a3)…(a3n-2)(a3n-1)(a3n) |
| 2 |
| 7 |
| 2 |
| 7 |
. | ||||||||||
t\~(
|
| lim |
| n→∞ |
| dn |
| dn+1 |
查看答案和解析>>
科目:高中数学 来源: 题型:
. |
| x\~(a1)(a2)(a3)…(an-1)(an) |
. |
| 2\~(-1)(3)(-2)(1) |
| 1 |
| 1-ak |
. |
| 2\~(a1)(a2)(a3)…(a3n-2)(a3n-1)(a3n) |
. | ||||||||||
t\~(
|
| lim |
| n→∞ |
| dn |
| dn+1 |
查看答案和解析>>
科目:高中数学 来源:江西省景德镇市2009届高三下学期第一次模拟质量检测(数学理) 题型:044
若数列{an}满足![]() -
-![]() =d,其中d为常数,则称数列{an}为等方差数列.已知等方差数列{an}满足an>0,a1=1,a1,a2,a5成等比数列且互不相等.
=d,其中d为常数,则称数列{an}为等方差数列.已知等方差数列{an}满足an>0,a1=1,a1,a2,a5成等比数列且互不相等.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)求数列![]() 的前n项和;
的前n项和;
(Ⅲ)是否存在实数m,使得对一切正整数n,总有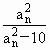 ≤m成立?若存在,求实数m的取值范围,若不存在,说明理由.
≤m成立?若存在,求实数m的取值范围,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
(14分)若数列![]() 满足
满足![]() ,其中
,其中![]() 为常数,则称数列
为常数,则称数列![]() 为等方差数列.已知等方差数列
为等方差数列.已知等方差数列![]() 满足
满足![]()
![]() 成等比数列且互不相等.
成等比数列且互不相等.
(Ⅰ)求数列![]() 的通项公式;
的通项公式;
(Ⅱ)求数列![]() 的前
的前![]() 项和;
项和;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com