
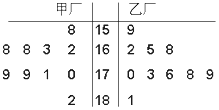
 ij��ҵ�������ֳ�����ij����������涨�ھ��ߴ磨��λ��mm�����������ڣ�164��181]�����Ϊ����Ʒ���ִ������ֳ��������������������10���������ھ��ߴ磨��λ��mm��������ھ��ߴ����ݵľ�Ҷͼ��ͼ��ʾ��
ij��ҵ�������ֳ�����ij����������涨�ھ��ߴ磨��λ��mm�����������ڣ�164��181]�����Ϊ����Ʒ���ִ������ֳ��������������������10���������ھ��ߴ磨��λ��mm��������ھ��ߴ����ݵľ�Ҷͼ��ͼ��ʾ������ �����ݾ�Ҷͼ�е����ݣ�����ס�����������Ʒ�ʣ�
���� ����n�ζ����ظ�ʵ��ĸ��ʹ�ʽ�����Ӧ�ĸ���ֵ��
���� ����֪�εĿ���ȡֵ��0��1��2�������Ӧ�ĸ��ʣ���д���εķֲ�������ѧ������
��� �⣺�����ݾ�Ҷͼ�е����ݣ�
�׳��������ڣ�164��181]���������Ϊ6������Ʒ��Ϊ$\frac{6}{10}$=0.6��
�ҳ��������ڣ�164��181]�����������8��������Ʒ��Ϊ$\frac{8}{10}$=0.8��---------��2�֣�
���� ���ҳ������������ȡ3�������
3�����ǡ��1��Ϊ����Ʒ�ĸ���Ϊ
P=$C_3^1����0.8����{��0.2��^2}$=0.096��--------------��6�֣�
���� ����֪�εĿ���ȡֵ��0��1��2��
��P����=0��=0.4��0.2=0.08��
P����=1��=0.6��0.2+0.4��0.8=0.44��
P����=2��=0.6��0.8=0.48��
�εķֲ���Ϊ
| �� | 0 | 1 | 4 |
| P | 0.08 | 0.44 | 0.48 |
���� ���⿼���˾�Ҷͼ�Լ�n�ζ����ظ�ʵ��ĸ��ʼ������⣬Ҳ�����˷ֲ�������ѧ�����ļ������⣬�ǻ����⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����ԲC��$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1��a��b��0����ԲO��x2+y2=b2����֪��ԲC��������Ϊ$\frac{{2\sqrt{2}}}{3}$��ֱ��$\sqrt{2}$x-2y-$\sqrt{6}$=0��ԲO���У�
��ͼ����ԲC��$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1��a��b��0����ԲO��x2+y2=b2����֪��ԲC��������Ϊ$\frac{{2\sqrt{2}}}{3}$��ֱ��$\sqrt{2}$x-2y-$\sqrt{6}$=0��ԲO���У��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | 2 | C�� | 4 | D�� | 8 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��������P-ABCD�У��ı���ABCDΪ���Σ�AB��BP��MΪAC���е㣬NΪPD��һ�㣮
��ͼ��������P-ABCD�У��ı���ABCDΪ���Σ�AB��BP��MΪAC���е㣬NΪPD��һ�㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com