
分析 bn=b1qn-1,bm=b1qm-1,可得qn-m=$\frac{{b}_{n}}{{b}_{m}}$,q=$(\frac{{b}_{n}}{{b}_{m}})^{\frac{1}{n-m}}$,利用bm+n=bmqn,可得结论.
解答 解:∵bn=b1qn-1,bm=b1qm-1,
∴qn-m=$\frac{{b}_{n}}{{b}_{m}}$,
∴q=$(\frac{{b}_{n}}{{b}_{m}})^{\frac{1}{n-m}}$
∴bm+n=bmqn=bm$(\frac{{b}_{n}}{{b}_{m}})^{\frac{n}{n-m}}$.
故答案为:bm+n=bm$(\frac{{b}_{n}}{{b}_{m}})^{\frac{n}{n-m}}$.
点评 本题考查类比思想,考查等比数列的通项的性质,考查学生分析解决问题的能力,属于基础题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
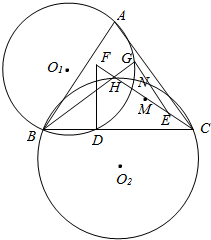 H为锐角三角形ABC的垂心,在线段CH上任取一点E,延长CH到F,使HF=CE,作FD⊥BC,EG⊥BH,其中D,G为垂足,M是线段CF的中点,O1,O2分别△ABG,△BCH的外接圆圆心,⊙O1,⊙O2的另一交点为N;证明:
H为锐角三角形ABC的垂心,在线段CH上任取一点E,延长CH到F,使HF=CE,作FD⊥BC,EG⊥BH,其中D,G为垂足,M是线段CF的中点,O1,O2分别△ABG,△BCH的外接圆圆心,⊙O1,⊙O2的另一交点为N;证明:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,2) | B. | (-2,2) | C. | (-1,2) | D. | (2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0<k<$\sqrt{2}$ | B. | 1<k<$\sqrt{2}$ | C. | 0<k<1 | D. | k>$\sqrt{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com