
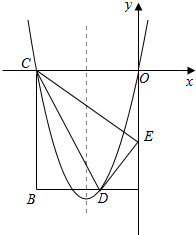
 ��ͼ���ھ���ABCD�У�OA=5��AB=4����DΪ��AB��һ�㣬����BCD��ֱ��CD�۵���ʹ��Bǡ������OA�ϵĵ�E�����ֱ���OC��OA���ڵ�ֱ��Ϊx�ᣬy�Ὠ��ƽ��ֱ������ϵ��
��ͼ���ھ���ABCD�У�OA=5��AB=4����DΪ��AB��һ�㣬����BCD��ֱ��CD�۵���ʹ��Bǡ������OA�ϵĵ�E�����ֱ���OC��OA���ڵ�ֱ��Ϊx�ᣬy�Ὠ��ƽ��ֱ������ϵ������ ��1�����۵������ʿ����CE��CO����Rt��COE�У��ɹ��ɶ��������OE����AD=m����Rt��ADE�У��ɹ��ɶ��������m��ֵ�������D�����꣬���C��O���㣬���ô���ϵ��������������߽���ʽ��
��2����t��ʾ��CP��BP�ij�����֤����DBP�ա�DEQ���ɵõ�BP=EQ�������t��ֵ��
��3�������N�����꣬�����������ENΪ�Խ��ߣ���EMΪ�Խ��ߣ���ECΪ�Խ��ߣ�����ƽ���ı��ε����ʿ���öԽ��ߵĽ�������꣬�Ӷ������M��ĺ����꣬�ٴ��������߽���ʽ�����M������꣮
��� �⣺��1����CE=CB=5��CO=AB=4��
����Rt��COE��OE=3��
��AD=m����DE=BD=4-m��
��OE=3��
��AE=5-3=2��
��Rt��ADE�У��ɹ��ɶ����ɵ�AD2+AE2=DE2����m2+22=��4-m��2�����m=$\frac{3}{2}$��
��D��-$\frac{3}{2}$��-5����
��C��-4��0����O��0��0����
�����O��D��C�����������Ϊy=ax��x+4����
��-5=-$\frac{3}{2}$a��-$\frac{3}{2}$+4�������a=$\frac{4}{3}$��
�������߽���ʽΪy=$\frac{4}{3}$x��x+4��=$\frac{4}{3}$x2+$\frac{16}{3}$x��
��2����CP=2t��
��BP=5-2t��
��Rt��DBP��Rt��DEQ��$\left\{\begin{array}{l}{DP=DQ}\\{BD=ED}\end{array}\right.$��
��Rt��DBP��Rt��DEQ��HL����
��BP=EQ��
��5-2t=t��
��t=$\frac{5}{3}$��
��3���������ߵĶԳ�Ϊֱ��x=-2��
����N��-2��n����
���������֪C��-4��0����E��0��-3����
��M��m��y����
�ٵ�ENΪ�Խ��ߣ����ı���ECNM��ƽ���ı���ʱ��
���߶�EN���е������Ϊ$\frac{0+��-2��}{2}$=-1���߶�CM�е������Ϊ$\frac{m-4}{2}$��
��EN��CM����ƽ�֣�
��$\frac{m-4}{2}$=-1�����m=2��
��M�����������ϣ�
��y=$\frac{4}{3}$��22+$\frac{16}{3}$��2=16��
��M��2��16����
�ڵ�EMΪ�Խ��ߣ����ı���ECMN��ƽ���ı���ʱ��
���߶�EM���е������Ϊ$\frac{m+0}{2}$���߶�CN�е������Ϊ$\frac{-2-4}{2}$=-3��
��EN��CM����ƽ�֣�
��$\frac{m}{2}$=-3�����m=-6��
�֡�M�����������ϣ�
��y=$\frac{4}{3}$����-6��2+$\frac{16}{3}$����-6��=16��
��M��-6��16����
�۵�CEΪ�Խ��ߣ����ı���EMCN��ƽ���ı���ʱ��
��MΪ�����ߵĶ��㣬��M��-2��-$\frac{16}{3}$����
���Ͽ�֪���������������ĵ�M��������Ϊ��2��16����-6��16����-2��-$\frac{16}{3}$����
���� ������Ҫ������κ������ۺ�Ӧ�ã��漰����ϵ������ȫ�������ε��ж������ʡ��۵������ʡ�ƽ���ı��ε����ʵ�֪ʶ�㣮�ڣ�1�������D�������ǽ���Ĺؼ����ڣ�2����֤��ȫ�ȣ��õ�����t�ķ����ǽ���Ĺؼ����ڣ�3����ע���������˼���Ӧ�ã����⿼��֪ʶ��϶࣬�ۺ��Խ�ǿ��


 ����ʦ��Сһ����ʦ������ҵϵ�д�
����ʦ��Сһ����ʦ������ҵϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ∅��A | B�� | 2��∅ | C�� | 3��A | D�� | {2}��A |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{{{3^{n+2}}-6n-9}}{4}$ | B�� | $\frac{{{3^{n+1}}-6n-9}}{4}$ | C�� | $\frac{{{3^{n+1}}+6n-9}}{4}$ | D�� | $\frac{{{3^n}+6n-9}}{4}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com