练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】如图，在正方体中， 为线段上的动点，则下列判断错误的是（ ）

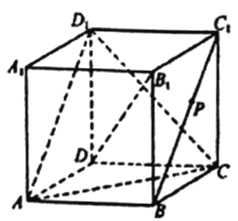
    A. 平面 B. 平面

    C. D. 三棱锥的体积与点位置有关

    【答案】D

    【解析】连接BD，则BD⊥AC，

    ∵BB1⊥面ABCD，∴DB1⊥AC，

    连接A1D，则A1D⊥AD1，

    ∵A1B1⊥面ADD1A1，∴DB1⊥AD1，

    ∴DB1⊥平面ACD1，故A正确；

    ∵BC1∥AD1，BC1面ACD1，AD1ACD1，

    ∴BC1∥平面ACD1，故B正确；

    ∵DB1⊥平面ACD1，AD1平面ACD1，

    ∴DB1⊥AD1，

    ∵BC1∥AD1，

    ∴BC1⊥DB1，故C正确；

    ∵BC1∥平面ACD1，P为线段BC1上的动点，

    ∴三棱锥P﹣ACD1的体积为定值，与P点位置无关，故D错误．

    故答案为：D．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=|x+2|+|x|
    （1）解不等式f（x）≤4；
    （2）若对x∈R，恒有f（x）＞|3a﹣1|成立，求a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某同学用“描点法”画函数在区间上的图象时,列表并填入了部分数据,如下表：

    (1)请将上表数据补充完整,并在给出的直角坐标系中,画出在区间上的图象；

    (2)利用函数的图象,直接写出函数在上的单调递增区间；

    (3)将图象上所有点向左平移个单位长度,得到的图象,若

    图象的一个对称中心为,求的最小值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】“共享单车”的出现，为我们提供了一种新型的交通方式．某机构为了调查人们对此种交通方式的满意度，从交通拥堵不严重的 城市和交通拥堵严重的 城市分别随机调查了20个用户，得到了一个用户满意度评分的样本，并绘制出茎叶图（如图所示）：

    合计

    认可

    不认可

    合计

    （Ⅰ）若得分不低于80分，则认为该用户对此种交通方式“认可”，否则认为该用户对此种交通方式“不认可”，请根据此样本完成此 列联表，并据此样本分析是否有 的把握认为城市拥堵与认可共享单车有关；
    （Ⅱ）若从此样本中的 城市和 城市各抽取1人，则在此2人中恰有一人认可的条件下，此人来自 城市的概率是多少？
    附：参考数据：（参考公式： ）

    0.150

    0.100

    0.050

    0.025

    0.010

    0.005

    0.001

    2.072

    2.706

    3.841

    5.024

    6.635

    10.828

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】下列给出的输入语句、输出语句和赋值语句：

    （1）输出语句INPUT ，b，c

    （2）输入语句INPUT =3

    （3）赋值语句3=A

    （4）赋值语句A=B=C

    则其中正确的个数是（ ）

    （A）0 （B）1 （C）2 （D）3

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某志愿者到某山区小学支教，为了解留守儿童的幸福感，该志愿者对某班40名学生进行了一次幸福指数的调查问卷，并用茎叶图表示如下（注：图中幸福指数低于70，说明孩子幸福感弱；幸福指数不低于70，说明孩子幸福感强）.

    （Ⅰ）根据茎叶图中的数据完成 列联表，并判断能否有 的把握认为孩子的幸福感强与是否是留守儿童有关？

    （Ⅱ）从15个留守儿童中按幸福感强弱进行分层抽样，共抽取5人，又在这5人中随机抽取2人进行家访，求这2个学生中恰有一人幸福感强的概率.
    参考公式： ； 附表：

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在三棱锥V-ABC中，平面VAB平面ABC， VAB为等边三角形，ACBC且AC=BC=，O,M分别为AB,VA的中点。

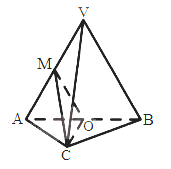
    （I）求证：VB//平面MOC；

    （II）求证：平面MOC平面VAB；

    （III）求三棱锥V-ABC的体积。

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】定义在R上的奇函数f（x）满足f（x﹣2）=f（x+2），且当x∈[﹣2，0]时，f（x）=3x﹣1，则f（9）=（ ）
    A.﹣2
    B.2
    C.
    D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在发生某公共卫生事件期间,有专业机构认为该事件在一段时间没有发生大规模群体感染的标准为“连续10天,每天新增疑似病例不超过7人”.根据过去10天甲、乙、丙、丁四地新增疑似病例的数据,一定符合该标准的是____.(填序号)

    ①甲地:总体均值为3,中位数为4

    ②乙地:总体均值为1,总体方差大于0

    ③丙地:中位数为2,众数为3

    ④丁地:总体均值为2,总体方差为3

    查看答案和解析>>

    同步练习册答案